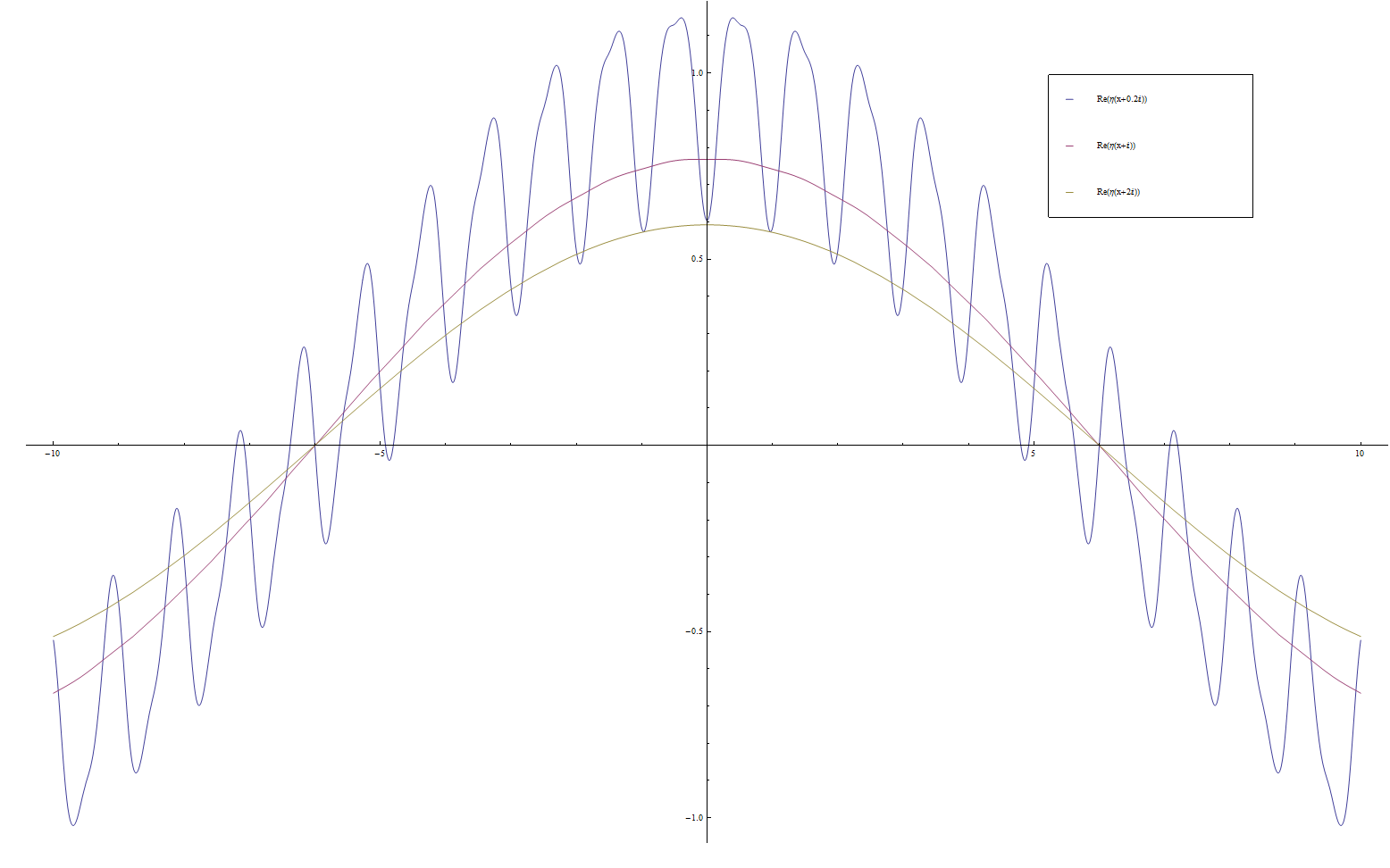
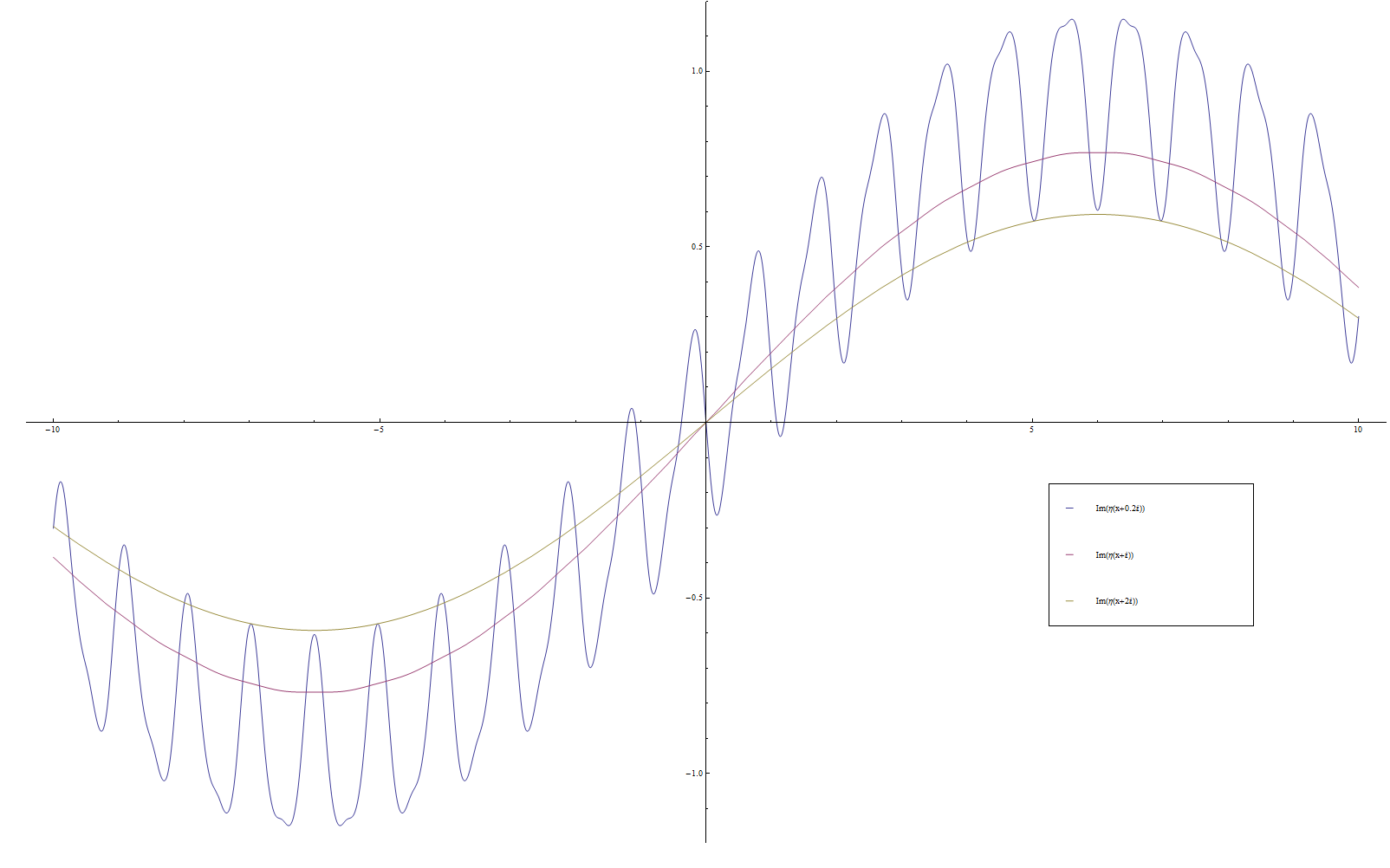
Dedekind eta

Let $q=e^{2\pi i \tau}$. We define the Dedekind eta function by the formula $$\eta(\tau) = e^{\frac{\pi i \tau}{12}} \displaystyle\prod_{n=1}^{\infty} (1-q^n).$$

• 

  Real part of $\eta$.

• 

  Imaginary part of $\eta$.

Properties

Theorem: The following formula holds for $\tau$ with $\mathrm{Im} \hspace{2pt} \tau > 0$: $$\eta \left( -\dfrac{1}{\tau} \right) = (-i\tau)^{\frac{1}{2}}\eta(\tau).$$

Proof: █

References

A collection of over 6200 identities for the Dedekind Eta Function