Thomae function
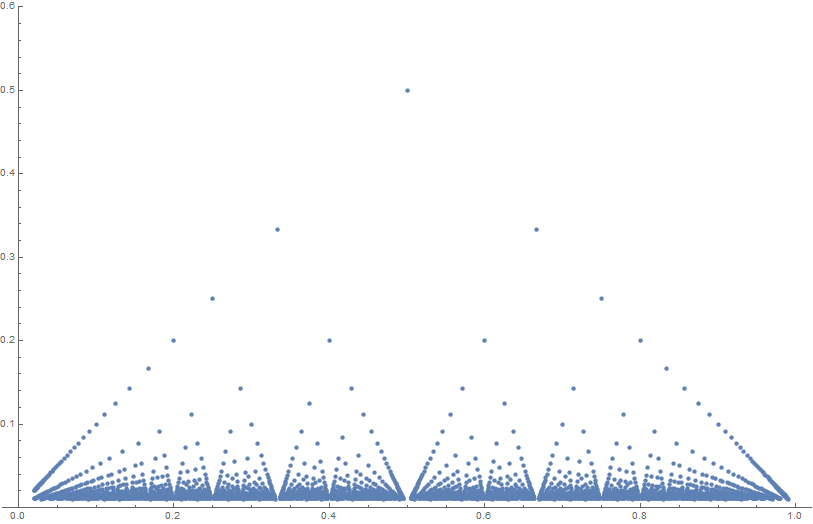
Thomae's function (sometimes called the popcorn function, raindrop function, Stars over Babylon) is given by the formula $$f(x) =\begin{cases} 1 & \text{if } x= 0 \\ \tfrac1{q} & \text{if } x = \tfrac{p}{q}\\ 0 & \text{if } x \in \mathbb{R}-\mathbb{Q}. \end{cases}$$
Plot of the Thomae function.
Properties
Theorem: The Thomae function is continuous at all irrational numbers and discontinuous at all rational numbers.
Proof: █
Theorem: The Thomae function has a (strict) local maximum at each rational number.
Proof: █
Theorem: The Thomae function $f(x)$ is Riemann integrable and $$\displaystyle\int_0^1 f(x) \mathrm{d}x = 0.$$
Proof: █
Videos
Thomae Function by Douglas Harder
Thomae Function by Bret Benesh
See also
Modifications of Thomae's Function and Differentiability
