Lambert W
From specialfunctionswiki
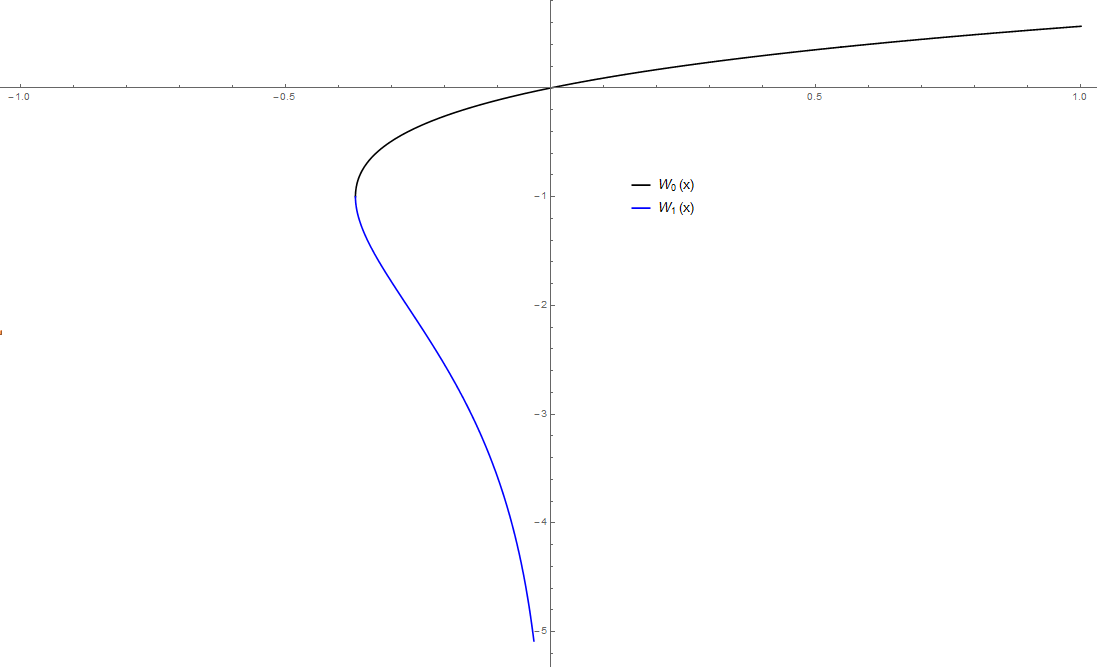
The Lambert $W$ function is the (multi-valued) inverse of the function $g(x)=xe^{x}$. The function $g$ is not injective because its graph does not pass the "horizontal line test". Therefore the inverse function is multi-valued and not unique. This yields two branches of the $W$ function.
Graph of branches $W_0(x)$ and $W_1(x)$ on $[-1,1]$.
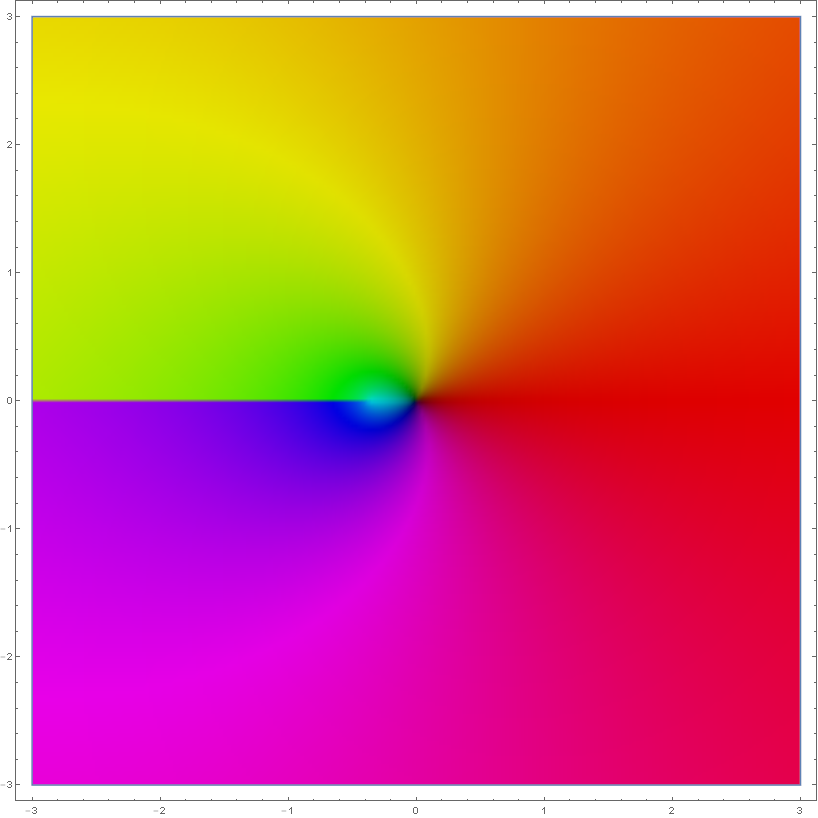
Domain coloring of analytic continuation of branch $W_0(x)$ to $\mathbb{C}$.
Domain coloring of analytic continuation of branch $W_{-1}(x)$ to $\mathbb{C}$.
