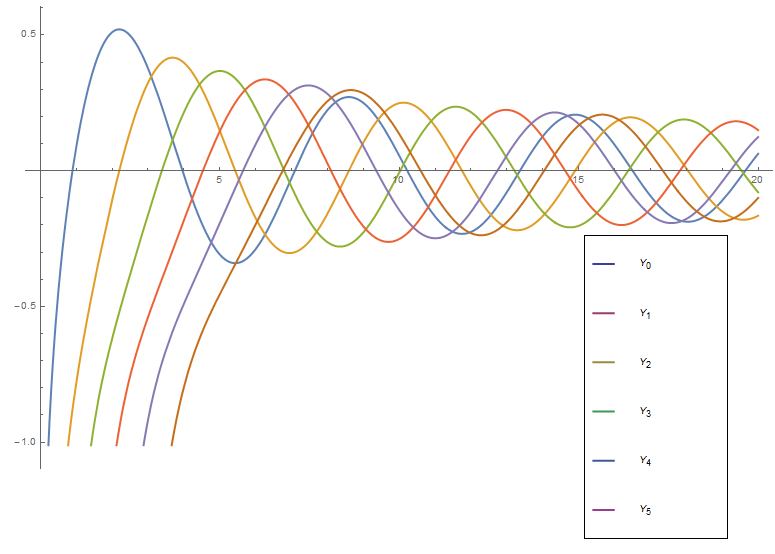
Bessel functions of the second kind $Y_{\nu}$ are defined via the formula $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.

Graph of $Y_0,Y_1,\ldots,Y_5$ on $[0,20]$.
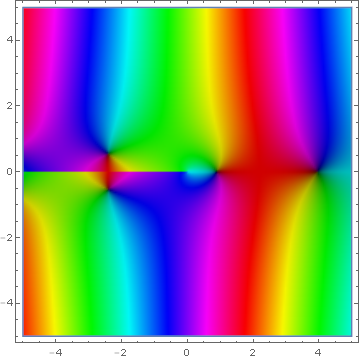
Domain coloring of analytic continuation of $Y_0(z)$.
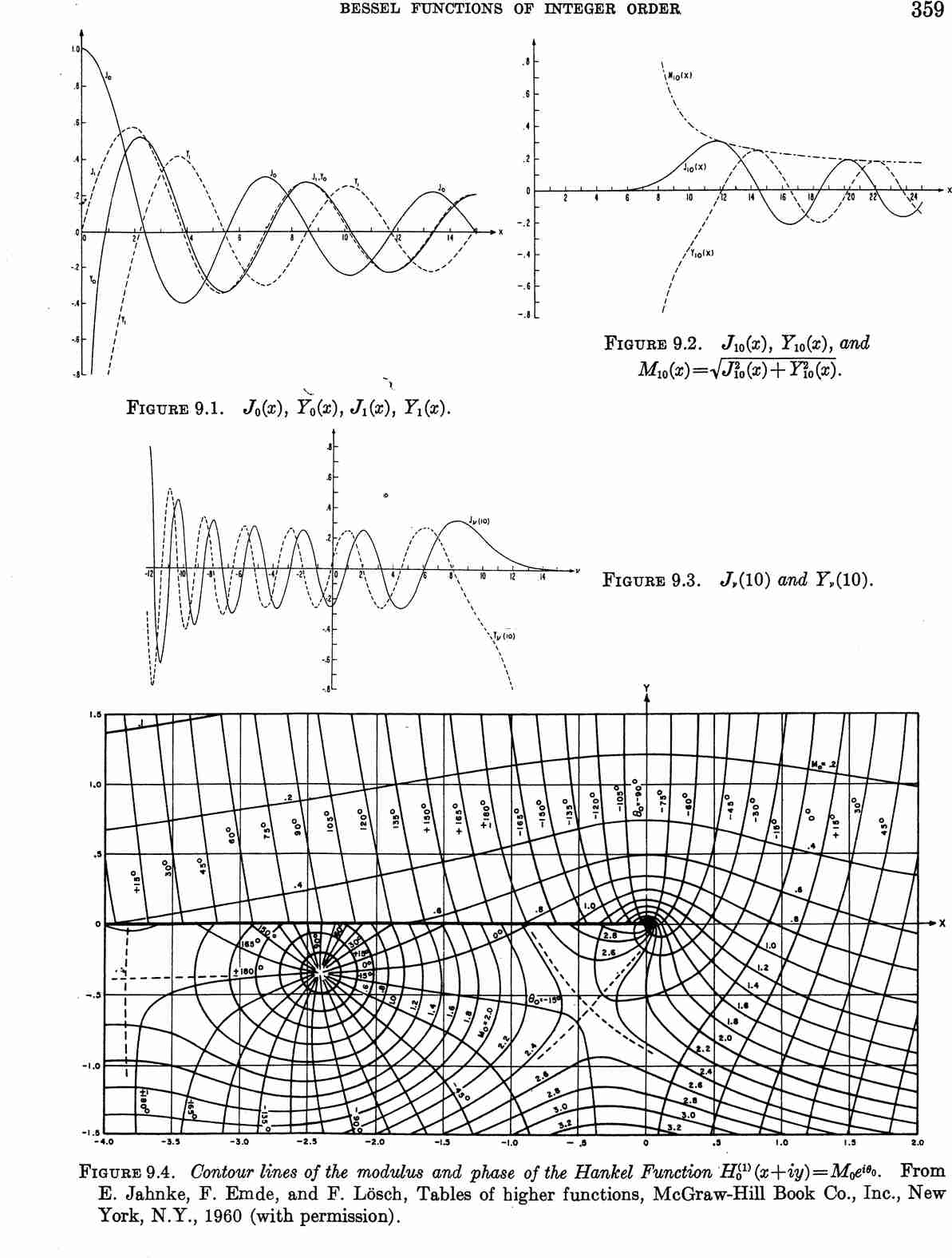
Bessel functions from Abramowitz&Stegun

Properties

Theorem: The following formula holds for $n \in \mathbb{Z}$: $$Y_{-n}(z)=(-1)^nY_n(z).$$

Proof: █

REDIRECT Bessel J and Y solve Bessel's differential equation

REDIRECT Bessel J and Y solve Bessel's differential equation (constant multiple in argument)

Theorem: The following formula holds for $n\in\mathbb{Z}$: $${\small Y_n(z)=\dfrac{2}{\pi} \left[ \log \left( \dfrac{z}{2} \right)+\gamma-\dfrac{1}{2}\displaystyle\sum_{k=1}^n \dfrac{1}{k} \right]J_n(x) - \dfrac{1}{\pi} \displaystyle\sum_{k=0}^{\infty} (-1)^k \dfrac{1}{k!(n+k)!} \left(\dfrac{z}{2}\right)^{n+2k}\displaystyle\sum_{j=1}^k \left( \dfrac{1}{j} + \dfrac{1}{j+n} \right) - \dfrac{1}{\pi}\displaystyle\sum_{k=0}^{n-1} \dfrac{(n-k-1)!}{k!} \left( \dfrac{z}{2} \right)^{-n+2k},}$$ where $Y_n$ denotes the Bessel function of the second kind, $\log$ denotes the logarithm, $\gamma$ denotes the Euler-Mascheroni constant, and $J_n$ denotes the Bessel function of the first kind.

Proof: █

<center>Bessel functions