Arcsinh
From specialfunctionswiki
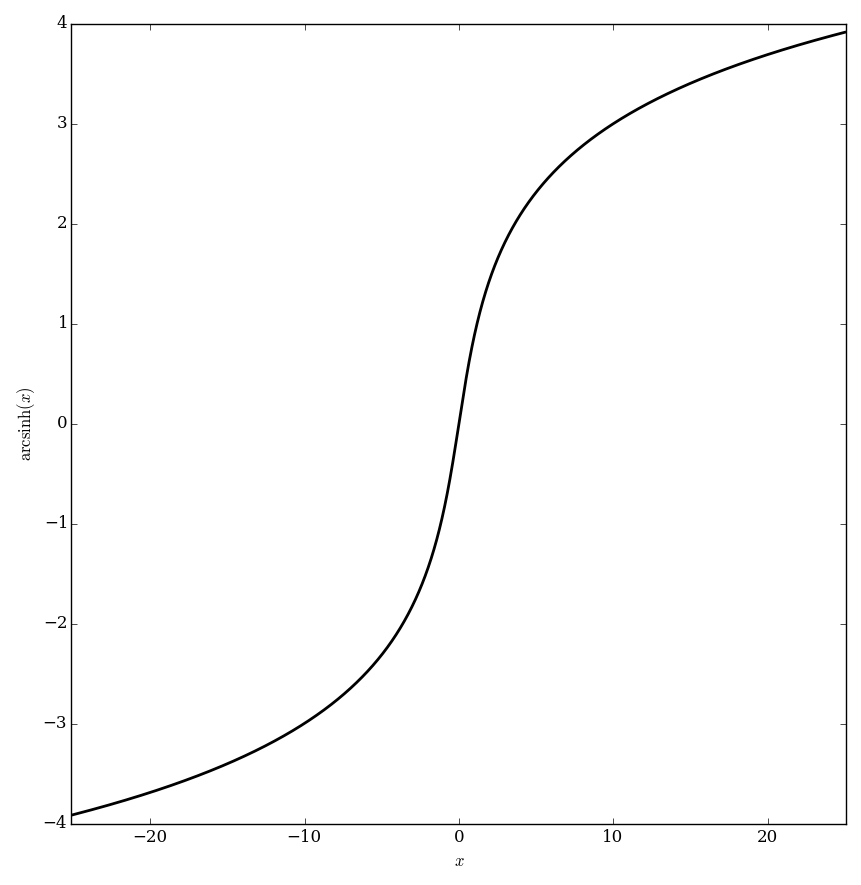
The $\mathrm{arcsinh}$ function is the inverse function of the hyperbolic sine function defined by $$\mathrm{arcsinh}(z)=\log\left(z+\sqrt{1+z^2}\right).$$
Plot of $\mathrm{arcsinh}$ on $[-10,10]$.
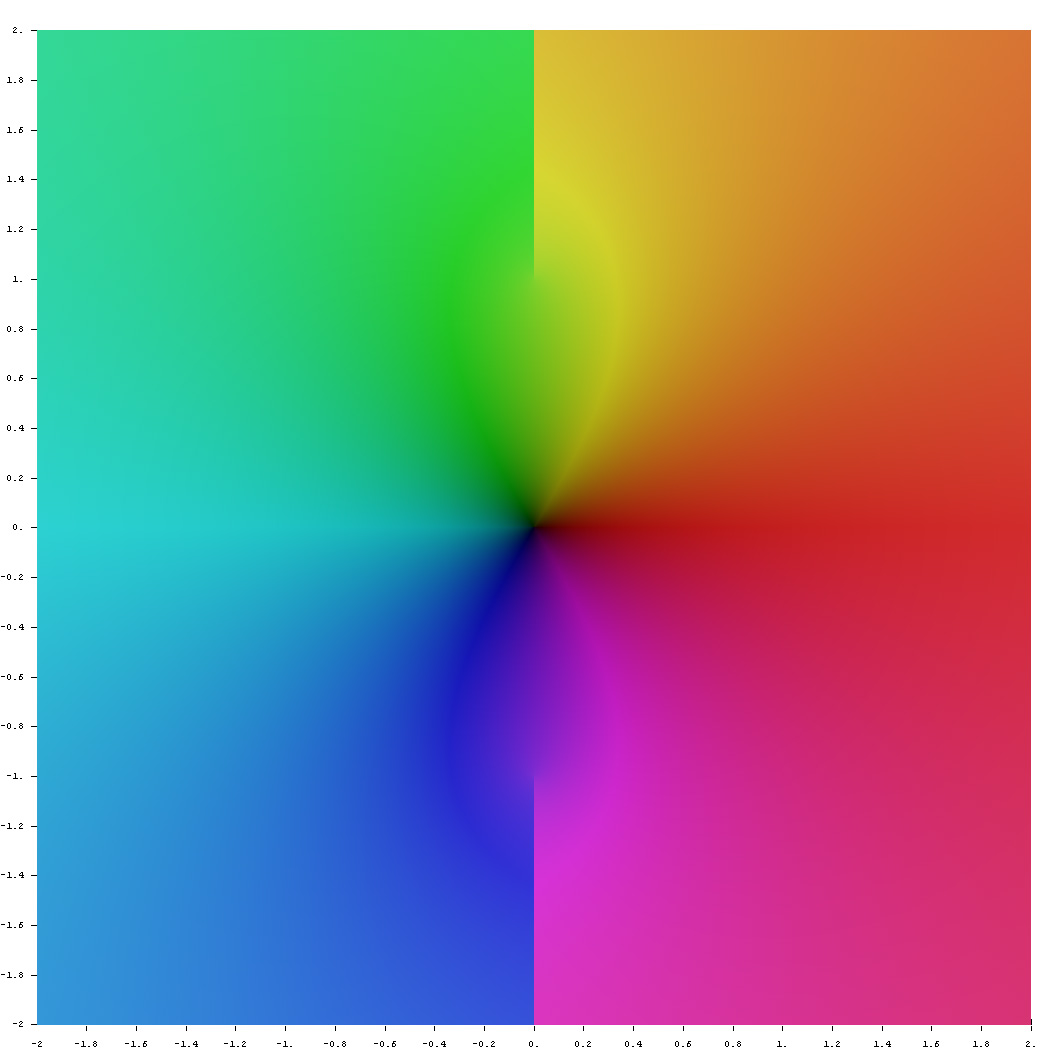
Domain coloring of analytic continuation of $\mathrm{arcsinh}$.
Properties
Theorem: The following formula holds: $$\dfrac{d}{dz} \mathrm{arcsinh}(z) = \dfrac{1}{\sqrt{1+z^2}}.$$
Proof: █
