Gamma
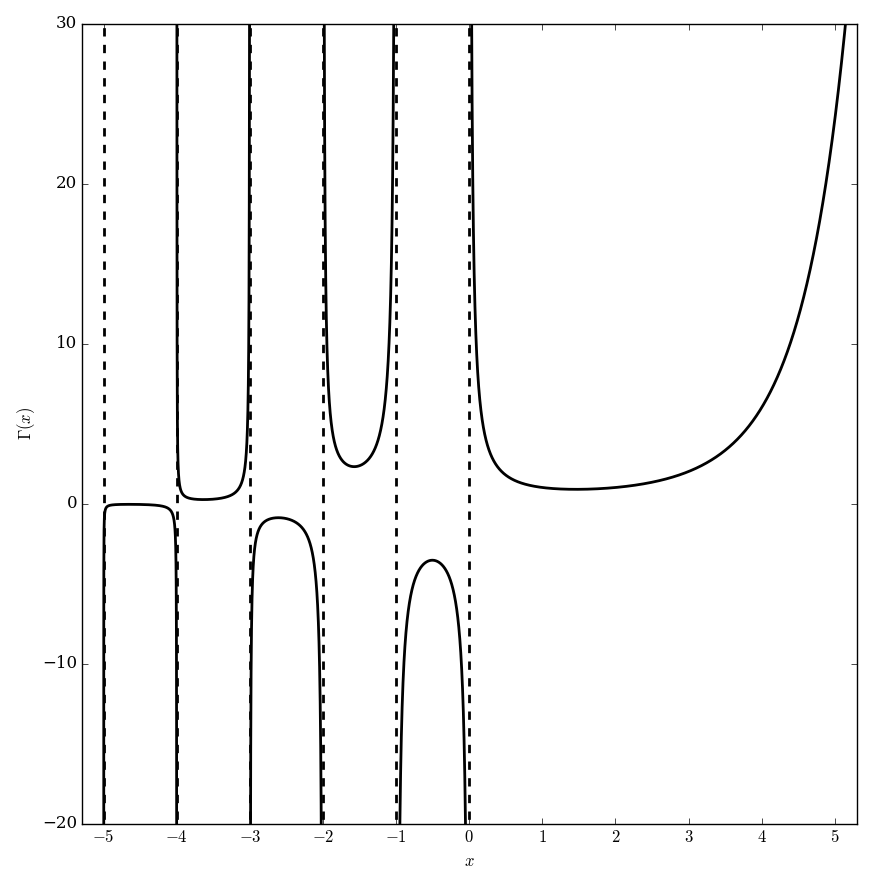
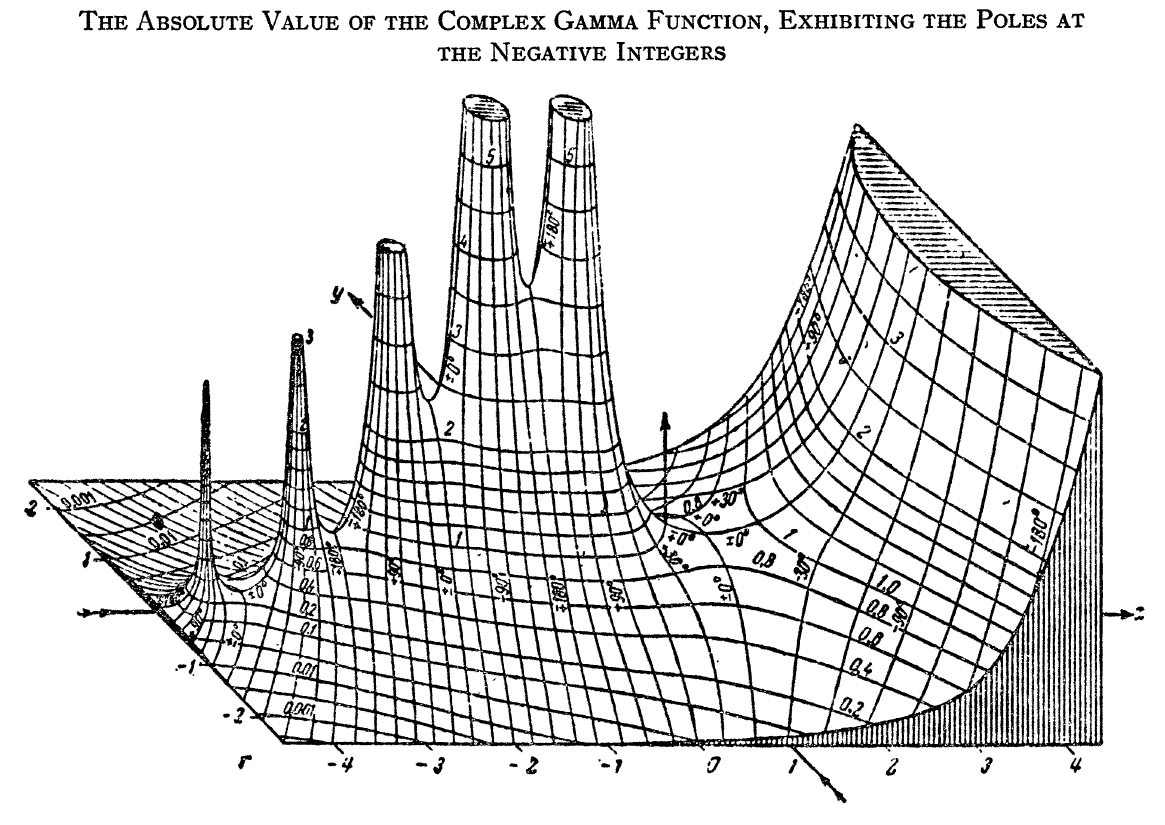
The gamma function is the function defined by the integral (initially for positive values of $x$) by the formula $$\Gamma(x)=\displaystyle\int_0^{\infty} \xi^{x-1}e^{-\xi} \mathrm{d}\xi.$$ The analytic continuation of $\Gamma$ leads to a meromorphic function with poles at the negative integers.
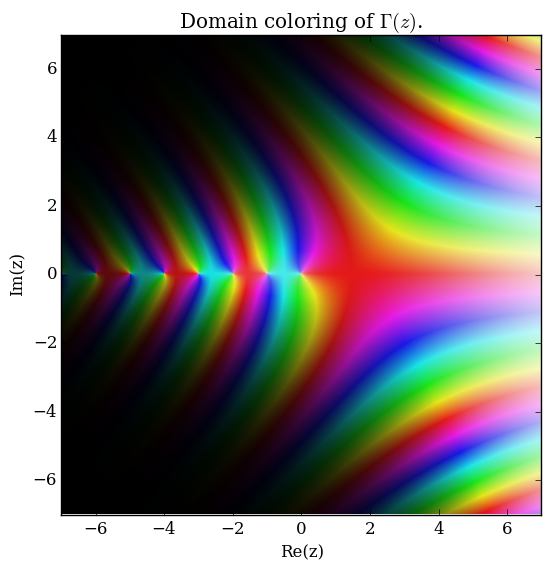
Domain coloring of $\Gamma$.
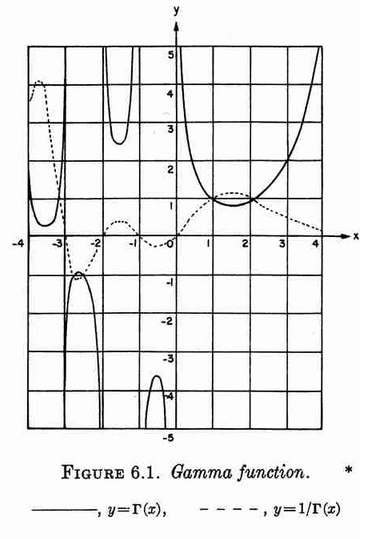
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
Contents
Properties
Theorem
The following formula holds: $$\Gamma(1)=1,$$ where $\Gamma$ denotes the gamma function.
Proof
Compute using the fundamental theorem of calculus, $$\begin{array}{ll} \Gamma(1) &= \displaystyle\int_0^{\infty} \xi^{0} e^{-\xi} \mathrm{d}\xi \\ &= \displaystyle\int_0^{\infty} e^{-\xi} \mathrm{d}\xi \\ &= \left[ -e^{-\xi} \right.\Bigg|_{0}^{\infty} \\ &= 1, \end{array}$$ as was to be shown. █
References
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): Theorem 2.1
Theorem
The following formula holds: $$\Gamma(z+1)=z\Gamma(z),$$ where $\Gamma$ denotes gamma.
Proof
Use integration by parts to compute $$\begin{array}{ll} \Gamma(z+1) &= \displaystyle\int_0^{\infty} \xi^z e^{-\xi} \mathrm{d}\xi \\ &= -\xi^z e^{-\xi}\Bigg|_0^{\infty}- \displaystyle\int_0^{\infty} z \xi^{z-1} e^{-\xi} \mathrm{d}\xi \\ &= z\Gamma(z), \end{array}$$ as was to be shown. █
References
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): Theorem 2.2
- 2010: Roelof Koekoek, Peter A. Lesky and René F. Swarttouw: Hypergeometric Orthogonal Polynomials and Their q-Analogues ... (previous) ... (next): $(1.2.2)$
- 2010: Richard Beals and Roderick Wong: Special functions, a graduate text ... (previous) ... (next): $(2.1.2)$
Theorem
If $n \in \{0,1,2,\ldots\}$, then $$\Gamma(n+1)=n!,$$ where $\Gamma$ denotes the gamma function and $n!$ denotes the factorial of $n$.
Proof
References
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): Theorem 2.3
Proposition: The following formula holds: $$\Gamma(x)=2\displaystyle\int_0^{\infty} e^{-t^2}t^{2x-1}dt.$$
Proof: █
Proposition: The following formula holds: $$\displaystyle\int_0^{\frac{\pi}{2}} \cos^{2x-1}(\theta)\sin^{2y-1}(\theta) d\theta = \dfrac{\Gamma(x)\Gamma(y)}{2\Gamma(x+y)}.$$
Proof: █
Theorem: The following formula holds for $\mathrm{Re}(z)>0$: $$\Gamma(z)=\displaystyle\int_0^1 \log \left( \dfrac{1}{t} \right)^{z-1} dt,$$ where $\Gamma$ denotes the gamma function and $\log$ denotes the logarithm.
Proof: █
Proposition: The following formula holds: $$\Gamma(z)=\lim_{k \rightarrow \infty} \dfrac{k!k^z}{z(z+1)\ldots(z+k)}.$$
Proof: █
Gamma function Weierstrass product
Theorem
The following formula holds: $$\Gamma(s)\zeta(s,a) = \displaystyle\int_0^{\infty} \dfrac{x^{s-1}e^{-ax}}{1-e^{-x}} \mathrm{d}x,$$ where $\Gamma$ denotes the gamma function and $\zeta$ denotes the Hurwitz zeta function.
Proof
References
Proposition: $\Gamma \left( \dfrac{1}{2} \right) = \sqrt{\pi}$.
Proof: █
Corollary: $\displaystyle\int_0^{\infty} e^{-t^2} dt = \dfrac{1}{2}\sqrt{\pi}$.
Theorem (Convexity): The gamma function is logarithmically convex.
Proof: █
Theorem (Legendre Duplication Formula): $$\Gamma(2x)=\dfrac{2^{2x-1}}{\sqrt{\pi}} \Gamma(x)\Gamma \left( x +\dfrac{1}{2} \right).$$
Proof: █
Proposition: If $z=0,-1,-2,\ldots$ then $\Gamma(z)=\infty$.
Proof: █
- REDIRECT Gamma(z)Gamma(1-z)=pi/sin(pi z)
Theorem
The gamma function is the unique function $f$ such that $f(1)=1$, $f(x+1)=xf(x)$ for $x>0$, and $f$ is logarithmically convex.
Proof
References
Theorem: The following formula holds: $$\displaystyle\lim_{t \rightarrow \infty} \dfrac{\Gamma(t+\alpha)}{\Gamma(t)t^{\alpha}}=\displaystyle\lim_{t \rightarrow \infty} \dfrac{\Gamma(t)t^{\alpha}}{\Gamma(t+\alpha)}=1.$$
Proof: proof goes here █
Videos
Gamma Function (playlist)
The Gamma Function: intro (5)
Gamma Integral Function - Introduction
Gamma function
Mod-04 Lec-09 Analytic continuation and the gamma function (Part I)
gamma function - Part 1
Beta Function, Gamma Function and their Properties
What's the Gamma Function?
euler gamma function
Thermodynamics 19 a : Gamma Function 1/2
The Gamma Function: why 0!=1 (5)
Gamma Function Of One-Half: Part 1
Gamma Function Of One-Half: Part 2
Gamma function at 1/2
Contour Integral Definition of the Gamma Function
See Also
Loggamma
Polygamma
Reciprocal gamma
References
The Gamma Function by Emil Artin
The sine product formula and the gamma function
Leonhard Euler's Integral: A Historical Profile of the Gamma Function