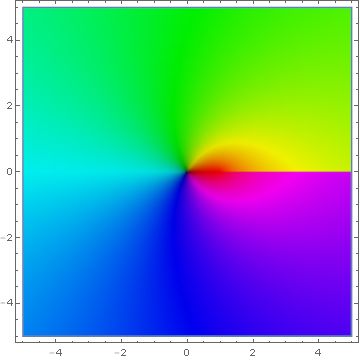
Dilogarithm
The dilogarithm function $\mathrm{Li}_2$ is defined for $|z| \leq 1$ by $$\mathrm{Li}_2(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{z^k}{k^2}; |z| \leq 1,$$ which is a special case of the polylogarithm.
Domain coloring of analytic continuation of the dilogarithm.
Properties
Relationship between dilogarithm and log(1-z)/z
Li 2(1)=pi^2/6
Relationship between Li 2(1),Li 2(-1), and pi
Relationship between Li 2(-1/x),Li 2(-x),Li 2(-1), and log^2(x)
Derivative of Li 2(-1/x)
Theorem: The following formula holds: $$\dfrac{d}{dx} \mathrm{Li}_2 \left( -\dfrac{1}{x} \right) = \dfrac{\log(1+\frac{1}{x})}{x}=\dfrac{\log(1+x)-\log x}{x}.$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(z)=-\mathrm{Li}_2 \left( \dfrac{1}{z} \right) - \dfrac{1}{2} \left( \log(z) \right)^2 + \pi i \log(z) + \dfrac{\pi^2}{3}.$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(x)+\mathrm{Li}_2(-x)=\dfrac{1}{2}\mathrm{Li}_2(x^2).$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(1-x)+\mathrm{Li}_2 \left(1-\dfrac{1}{x} \right)=-\dfrac{1}{2}\left( \log x \right)^2.$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(x)+\mathrm{Li}_2(1-x)=\dfrac{\pi^2}{6} - (\log x) \log(1-x).$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(-x)-\mathrm{Li}_2(1-x)+\dfrac{1}{2}\mathrm{Li}_2(1-x^2)=-\dfrac{\pi^2}{12} - (\log x) \log(x+1).$$
Proof: █
References
- 1926: Leonard Lewin: Polylogarithms and Associated Functions (2nd ed.) ... (next): (1.1)