Arcsin
From specialfunctionswiki
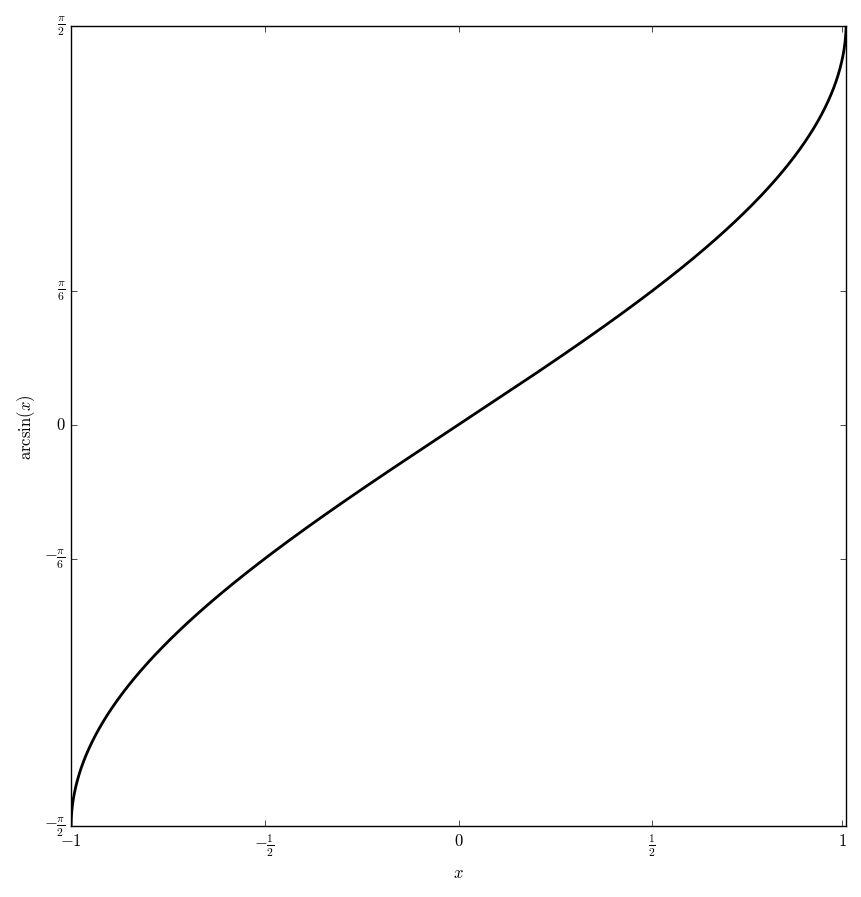
The function $\mathrm{arcsin} \colon [-1,1] \rightarrow \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$ is the inverse function of the sine function.
Domain coloring of $\mathrm{arcsin}$.
Contents
Properties
Derivative of arcsin
Antiderivative of arcsin
Relationship between arcsin and arccsc
Proposition: $\mathrm{arcsin}(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{\left(\frac{1}{2} \right)_n}{(2n+1)n!}x^{2n+1}$
Proof: █
Relationship between arcsin and hypergeometric 2F1
Videos
Inverse Trig Functions: Arcsin
Integrate x*arcsin(x)
What is arcsin(x)?
What is the inverse of arcsin(ln(x))?
See Also
References
On the function arc sin(x+iy)-Cayley