Derivative of arcsin

Theorem

The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsin(z)} = \dfrac{1}{\sqrt{1-z^2}},$$ where $\arcsin$ denotes the inverse sine function.

Proof

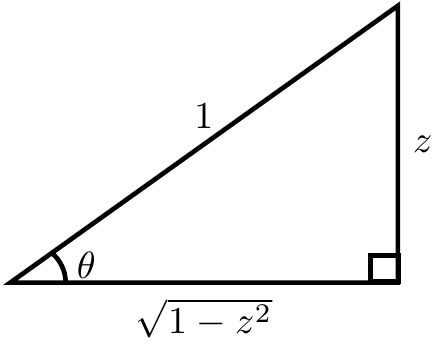
If $\theta=\mathrm{arcsin}(z)$ then $\sin(\theta)=z$. Now use implicit differentiation with respect to $z$ to get $$\cos(\theta)\theta'=1.$$ The following image shows that $\cos(\mathrm{arcsin}(z))=\sqrt{1-z^2}$:

Hence substituting back in $\theta=\mathrm{arccos}(z)$ yields the formula $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsin(z)} = \dfrac{1}{\cos(\mathrm{arcsin(z)})} = \dfrac{1}{\sqrt{1-z^2}},$$ as was to be shown. █