Prime counting

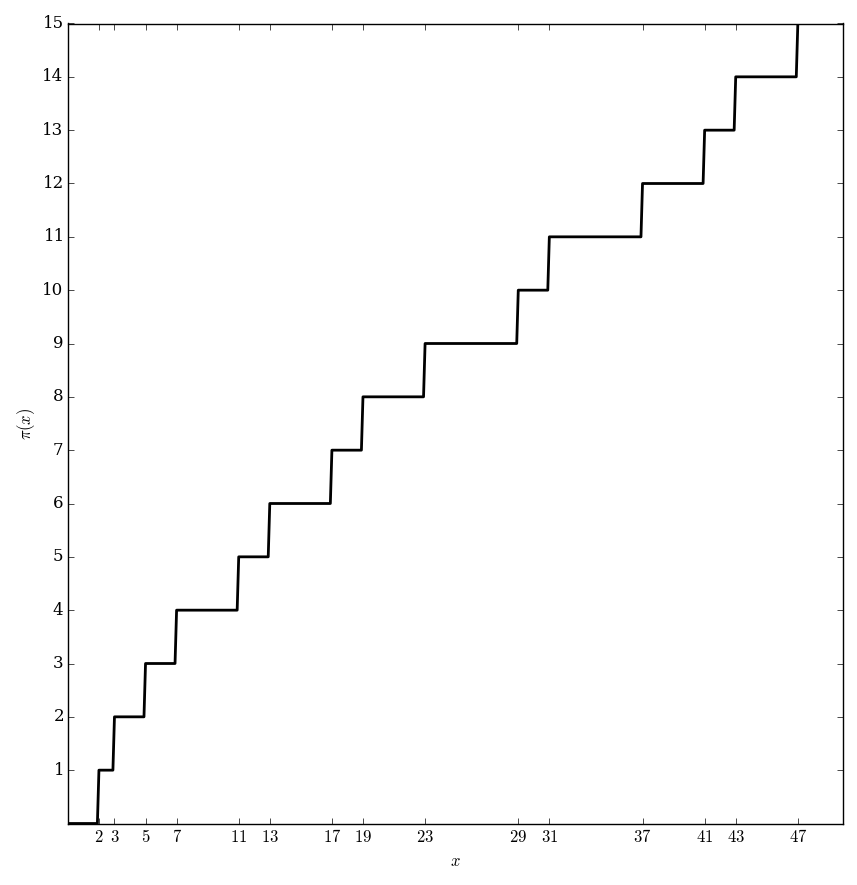
The prime counting function $\pi \colon \mathbb{R} \rightarrow \mathbb{Z}^+$ is defined by the formula $$\pi(x) = \{\mathrm{number \hspace{2pt} of \hspace{2pt} primes} \leq x \}.$$

• 

  Graph of $\pi(x)$.

Properties

Prime number theorem, pi and x/log(x) Prime number theorem, logarithmic integral

References

Newman's short proof of the prime number theorem