Modified Bessel I

The modified Bessel function of the first kind is defined by $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz),$$ where $J_{\nu}$ is the Bessel function of the first kind.

• 

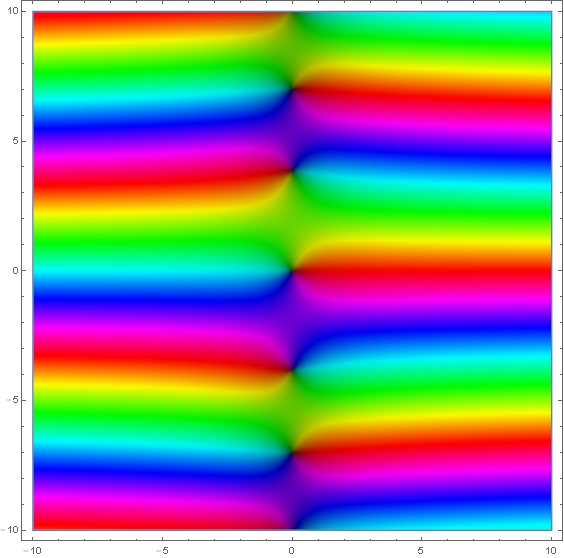
  Domain coloring of analytic continuation of $I_1(z)$.

• 

  Modified Bessel functions from Abramowitz&Stegun.

Properties

Relationship between Bessel I sub -1/2 and cosh
Relationship between Bessel I sub 1/2 and sinh
Relationship between Bessel I sub n and Bessel J sub n
Relationship between Airy Bi and modified Bessel I

Proposition: The following formula holds: $$I_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} J_{\nu+k}(z) \dfrac{z^k}{k!},$$ where $J_{\nu}$ denotes the Bessel function of the first kind.

Proof: █

<center>Bessel functions

Anger function

Bessel-Clifford

Bessel $J_{\nu}$

Bessel $Y_{\nu}$

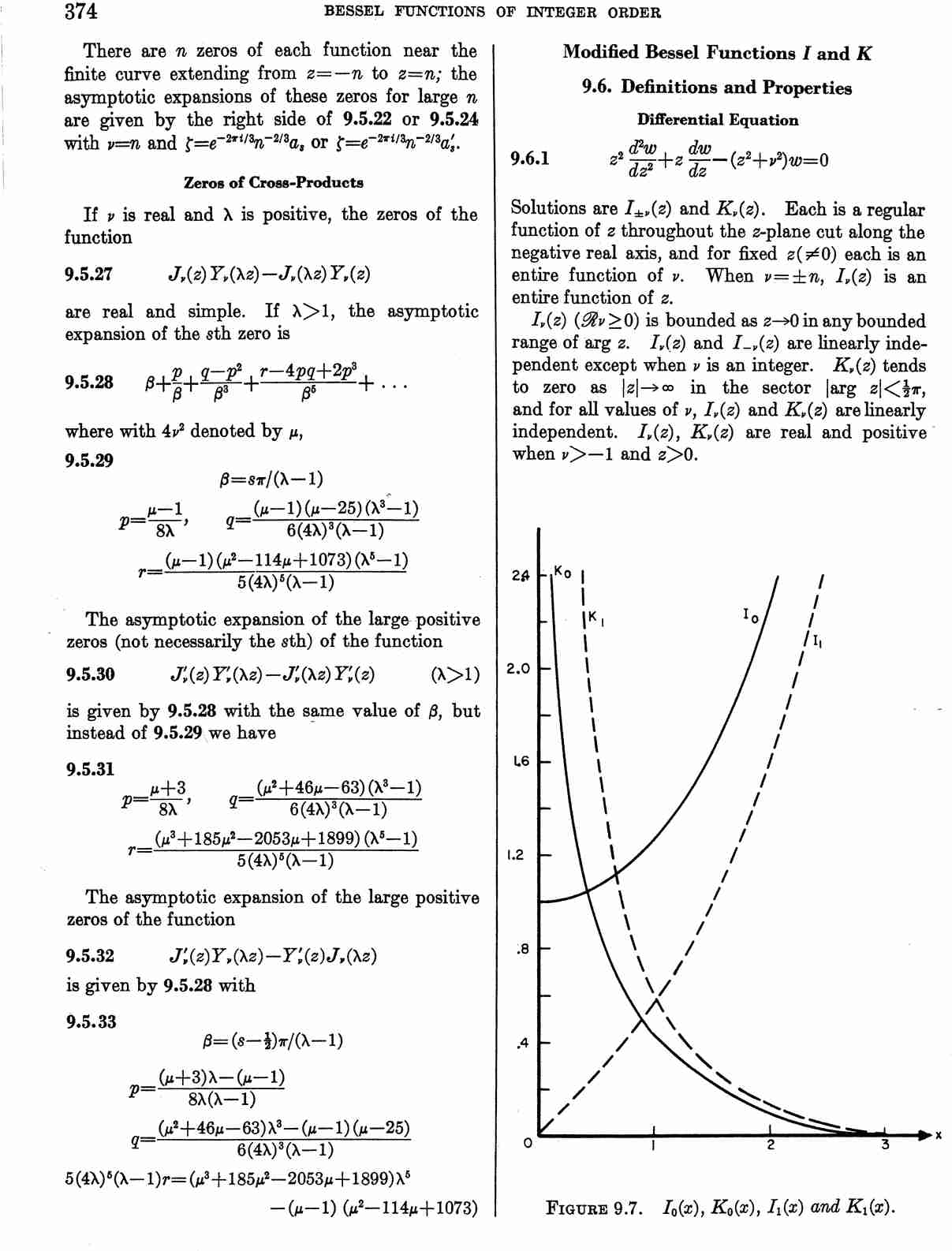
Bessel $I_{\nu}$

Modified Bessel $K_{\nu}$

Spherical Bessel $j_{\nu}$

Spherical Bessel $y_{\nu}$

</center>

References

[1]