Gamma
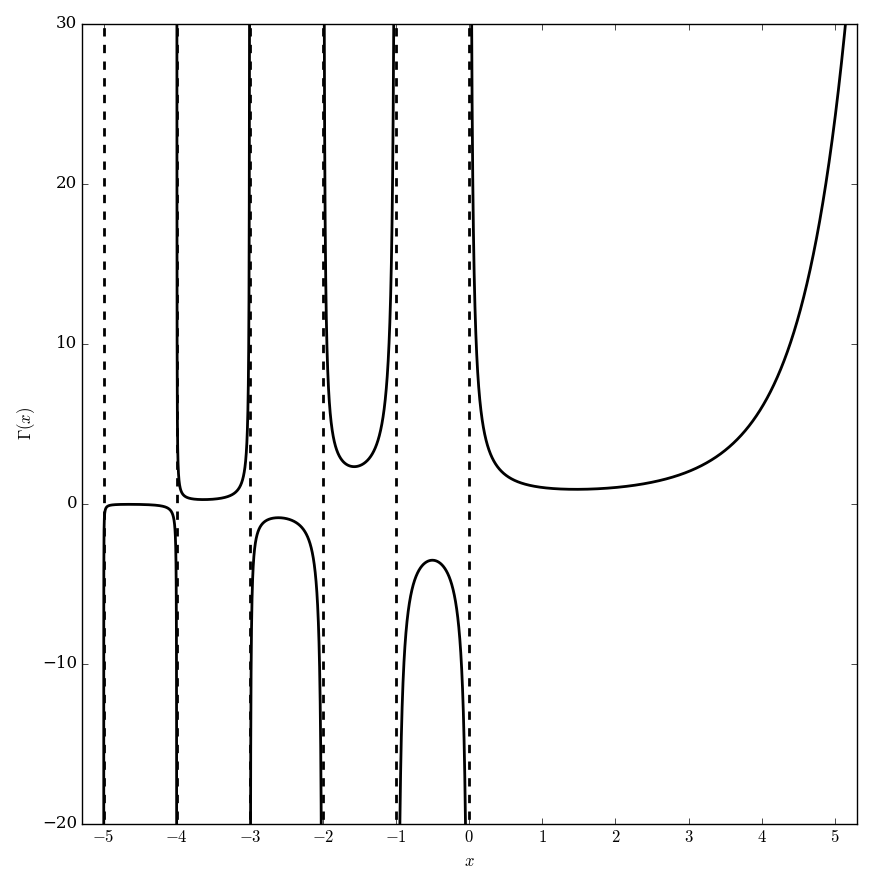
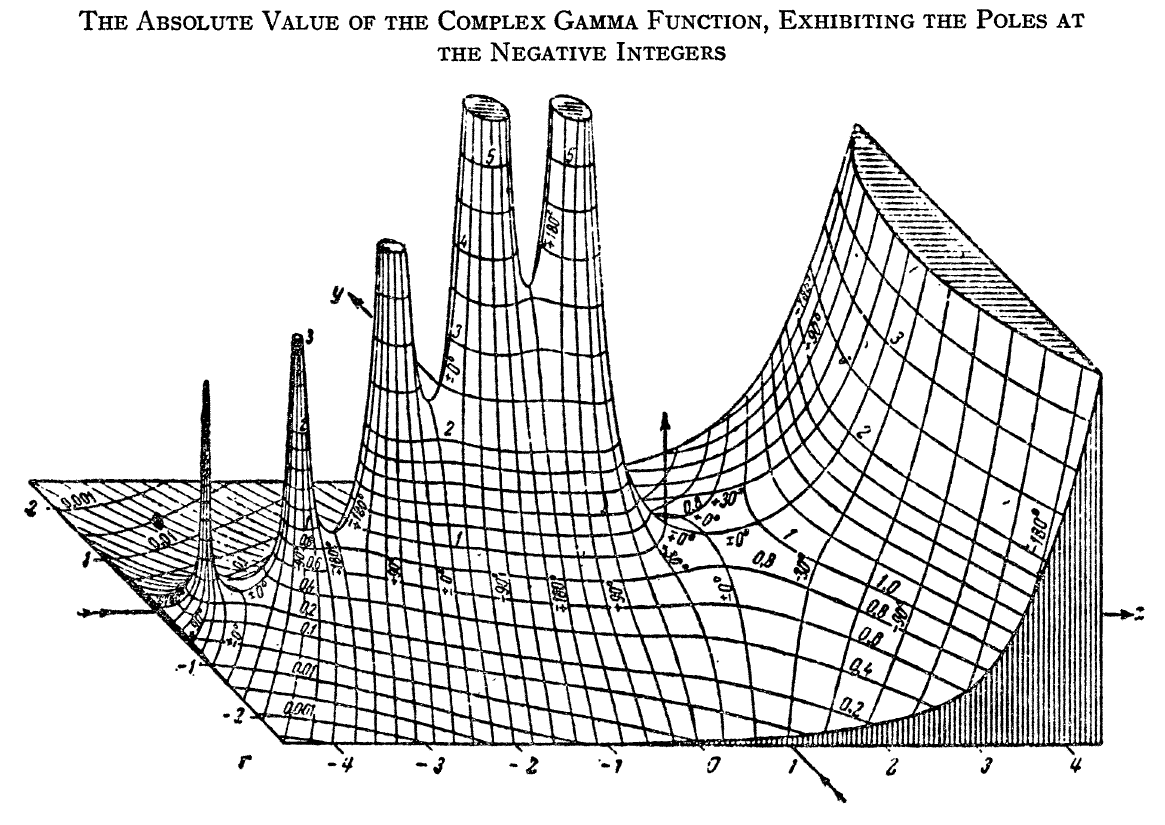
The gamma function $\Gamma \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is the function initially defined for $\mathrm{Re}(z)>0$ by the integral by the formula $$\Gamma(x)=\displaystyle\int_0^{\infty} \xi^{x-1}e^{-\xi} \mathrm{d}\xi.$$ The analytic continuation of $\Gamma$ leads to a meromorphic function with poles at the negative integers.
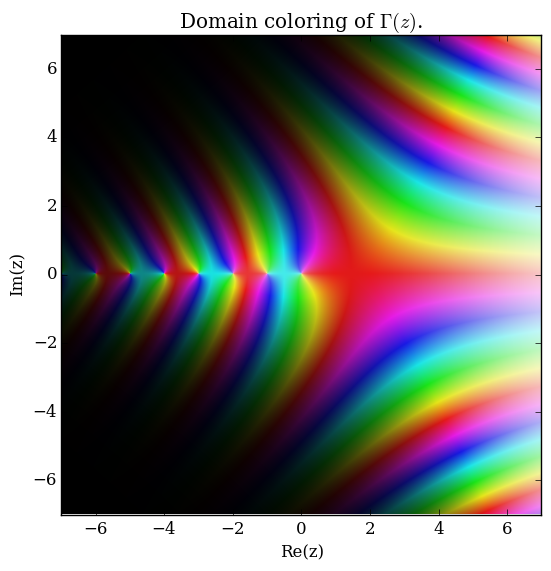
Domain coloring of $\Gamma$.
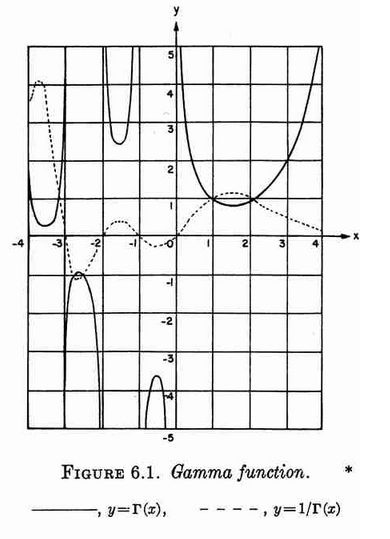
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
Contents
Properties
Gamma(z) as integral of a power of log(1/t) for Re(z) greater than 0
Gamma function written as a limit of a factorial, exponential, and a rising factorial
Gamma function written as infinite product
Value of Gamma(1)
Factorial property of gamma
Gamma at positive integers
Gamma function Weierstrass product
Relationship between Hurwitz zeta and gamma function
Gamma-Sine Relation
Bohr-Mollerup theorem
Videos
Gamma Function (playlist)
The Gamma Function: intro (5)
Gamma Integral Function - Introduction
Gamma function
Mod-04 Lec-09 Analytic continuation and the gamma function (Part I)
gamma function - Part 1
Beta Function, Gamma Function and their Properties
What's the Gamma Function?
euler gamma function
Thermodynamics 19 a : Gamma Function 1/2
The Gamma Function: why 0!=1 (5)
Gamma Function Of One-Half: Part 1
Gamma Function Of One-Half: Part 2
Gamma function at 1/2
Contour Integral Definition of the Gamma Function
See Also
Loggamma
Polygamma
Reciprocal gamma
References
- 1920: Edmund Taylor Whittaker and George Neville Watson: A course of modern analysis ... (previous) ... (next): $\S 12 \cdot 1$
- 1953: Harry Bateman: Higher Transcendental Functions Volume I ... (next): §1.1 (1)
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 6.1.1
The sine product formula and the gamma function
Leonhard Euler's Integral: A Historical Profile of the Gamma Function