Euler totient
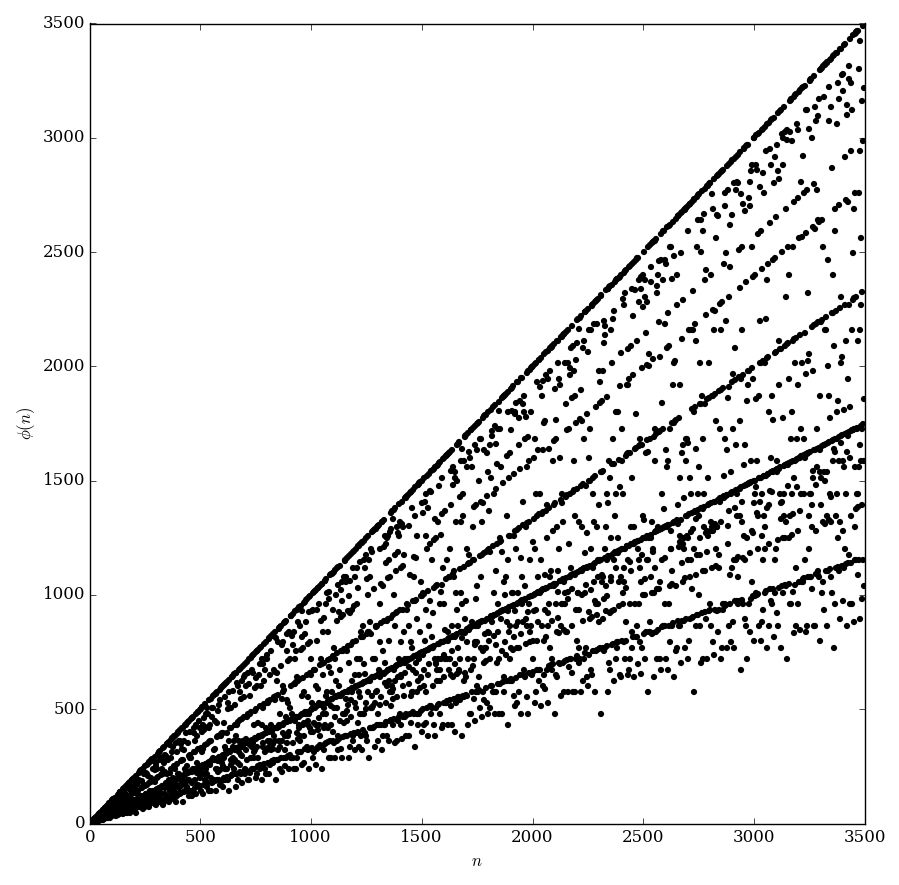
Euler's totient function $\phi$ (not to be confused with the Euler phi) is defined for $n=1,2,3,\ldots$ so that $\phi(n)$ equals the number of positive integers less than or equal to $n$ that are relatively prime to $n$.
Graph of $\phi$.
Properties
Videos
Euler's Totient Function: what it is and how it works
Euler's Totient Theorem: What is Euler's Totient Theorem and Why is it useful?
Euler's Totient Function | How To Find Totient Of A Number Using Euler's Product Formula
Euler's Totient Function
Euler's totient function
Prime Factorisation and Euler Totient Function Part 14
Application of Euler Totient Function Part 16
Möbius and Euler totient functions
Euler Totient Theorem, Fermat Little Theorems
Euler's Phi Function
03 Modern cryptography 08 Euler's totient function
