Dirichlet beta
From specialfunctionswiki
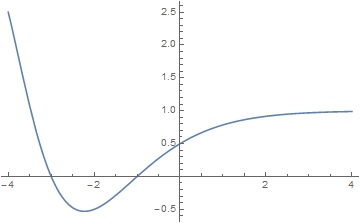
The Dirichlet $\beta$ function is defined by $$\beta(x) = \displaystyle\sum_{k=0}^{\infty} (-1)^k (2k+1)^{-x} = 2^{-x} \Phi \left(-1,x,\dfrac{1}{2} \right),$$ where $\Phi$ denotes the Lerch transcendent.
Graph of $\beta$ on $[-4,4]$.
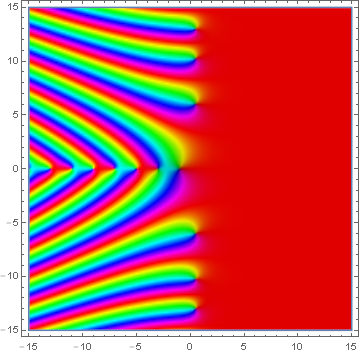
Domain coloring of analytic continuation of $\beta$.
