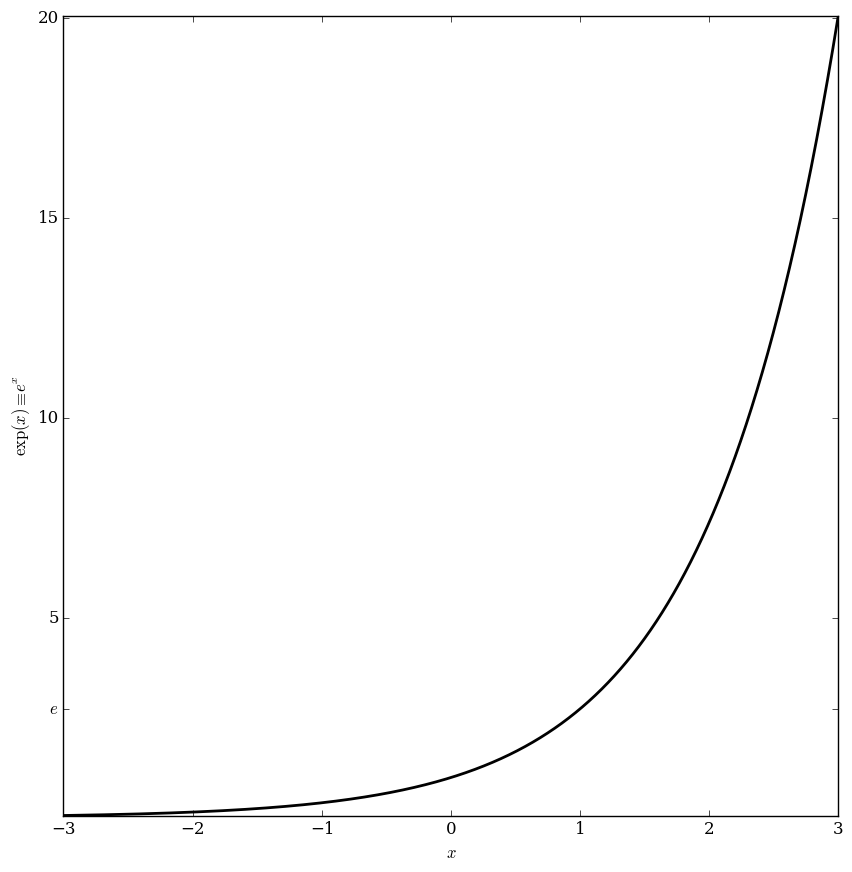
Exponential
The exponential function $\exp \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula
$$\exp(z) = e^z = \sum_{k=0}^{\infty} \dfrac{z^k}{k!},$$
where $e$ is the base of the natural logarithm.
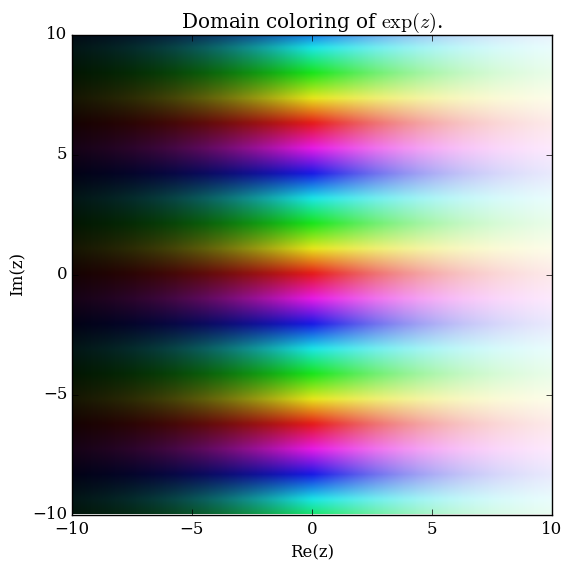
Domain coloring of $\exp$.
Properties
Derivative of the exponential function
Taylor series of the exponential function
Euler E generating function
Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt
Exponential function is periodic with period 2pii
Euler's formula
E^(-x/(1-x)) is less than 1-x is less than e^(-x) for nonzero real x less than 1
E^x is greater than 1+x for nonzero real x
E^x is less than 1/(1-x) for nonzero real x less than 1
X/(1+x) less than 1-e^(-x) less than x for nonzero real x greater than -1
X less than e^x-1 less than x/(1-x) for nonzero real x less than 1
1+x greater than exp(x/(1+x)) for nonzero real x greater than -1
E^x greater than 1+x^n/n! for n greater than 0 and nonzero real x greater than 0
E^x greater than (1+x/y)^y greater than exp(xy/(x+y) for x greater than 0 and y greater than 0)
E^(-x) less than 1-(x/2) for 0 less than x less than or equal to 1.5936
Abs(z)/4 less than abs(e^z-1) less than (7abs(z))/4 for 0 less than abs(z) less than 1
Abs(e^z-1) less than or equal to e^(abs(z))-1 less than or equal to abs(z)e^(abs(z))
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.2.1