Chi

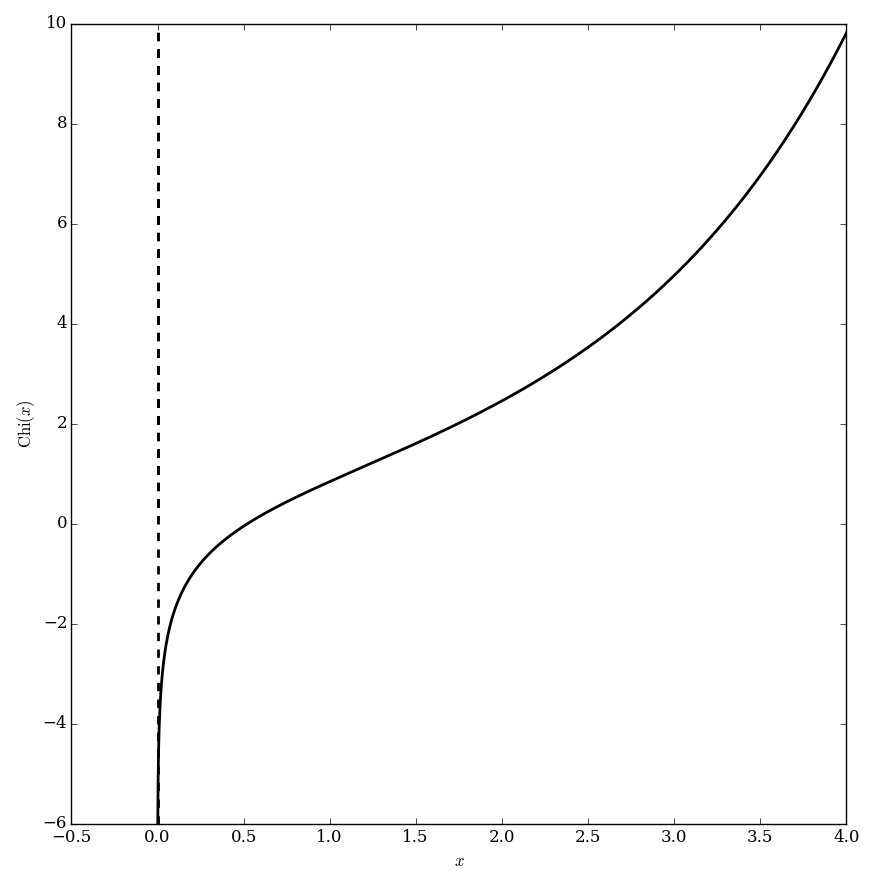
The hyperbolic cosine integral $\mathrm{Chi} \colon (0,\infty) \rightarrow \mathbb{R}$ is defined by the formula $$\mathrm{Chi}(z)=-\displaystyle\int_z^{\infty} \dfrac{\mathrm{cosh}(t)}{t} \mathrm{d}t,$$ where $\cosh$ denotes the hyperbolic cosine.

• 

  Graph of $\mathrm{Chi}$.

• 

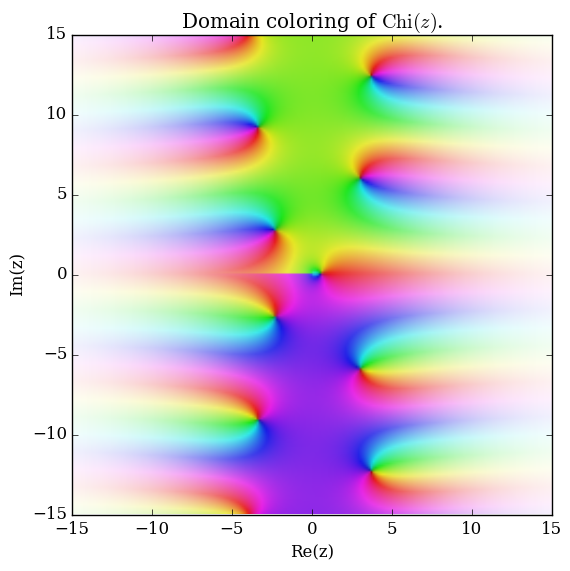
  Domain coloring of $\mathrm{Chi}$.

Properties

Derivative of chi
Antiderivative of chi

$\ast$-integral functions

Cosine integral

Cosh integral

Exp integral $E_n$

Exp integral $\mathrm{Ei}$

Fresnel $C$

Fresnel $S$

Gudermannian

Inverse $\mathrm{gd}$

Sine integral

Log integral

Sinh integral