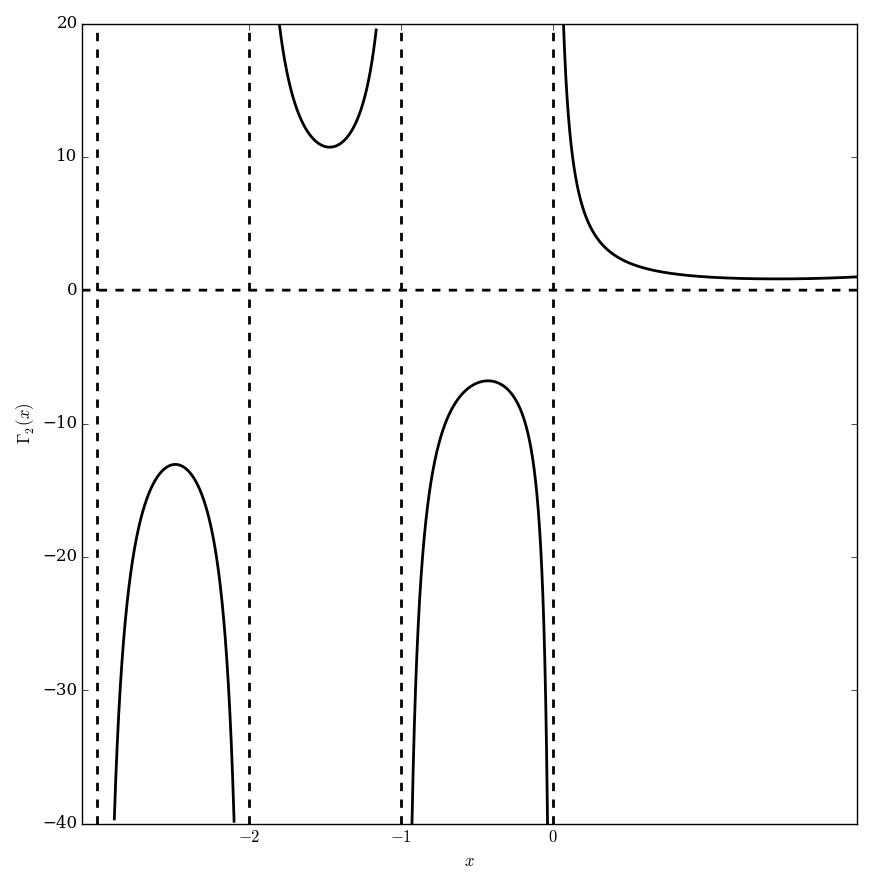
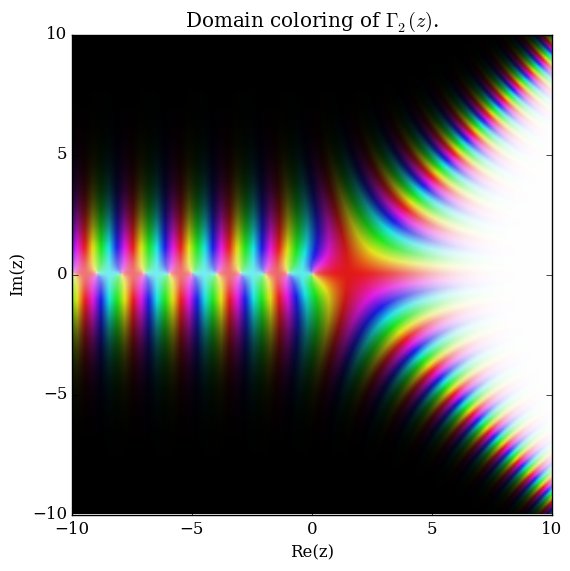
Q-Gamma
Let $0<q<1$. Define the $q$-gamma function by the formula $$\Gamma_q(z) = \dfrac{(q;q)_{\infty}}{(q^z;q)_{\infty}}(1-q)^{1-z},$$ where $(\cdot;\cdot)_{\infty}$ denotes the q-factorial. The function $\Gamma_q$ is a $q$-analogue of the gamma function.
Domain coloring of $\Gamma_2$.
Properties
q-Gamma at z+1
q-Gamma at 1
q-Gamma at 2
Theorem ($q$-Bohr-Mollerup): Let $f$ be a function which satisfies $$f(x+1) = \dfrac{1-q^x}{1-q}f(x)$$ for some $q \in (0,1)$, $$f(1)=1,$$ and $\log f(x)$ is convex for $x>0$. Then $f(x) = \Gamma_q(x)$.
Proof: █
Theorem (Legendre Duplication Formula): $\Gamma_q(2x)\Gamma_{q^2}\left(\dfrac{1}{2}\right)=\Gamma_{q^2}(x)\Gamma_{q^2}\left( x +\dfrac{1}{2} \right)(1+q)^{2x+1}$
Proof: proof goes here █
Theorem: ($q$-analog) The following formula holds: $$\displaystyle\lim_{q \rightarrow 1^-} \Gamma_q(z) = \Gamma(z),$$ where $\Gamma_q$ is the q-Gamma function and $\Gamma$ is the gamma function.
Proof: █
References
- Richard Askey: The q-Gamma and q-Beta functions (1978)... (next)
- Daniel S. Moak: The q-gamma function for q greater than 1 (1980)... (next)