Elliptic K
From specialfunctionswiki
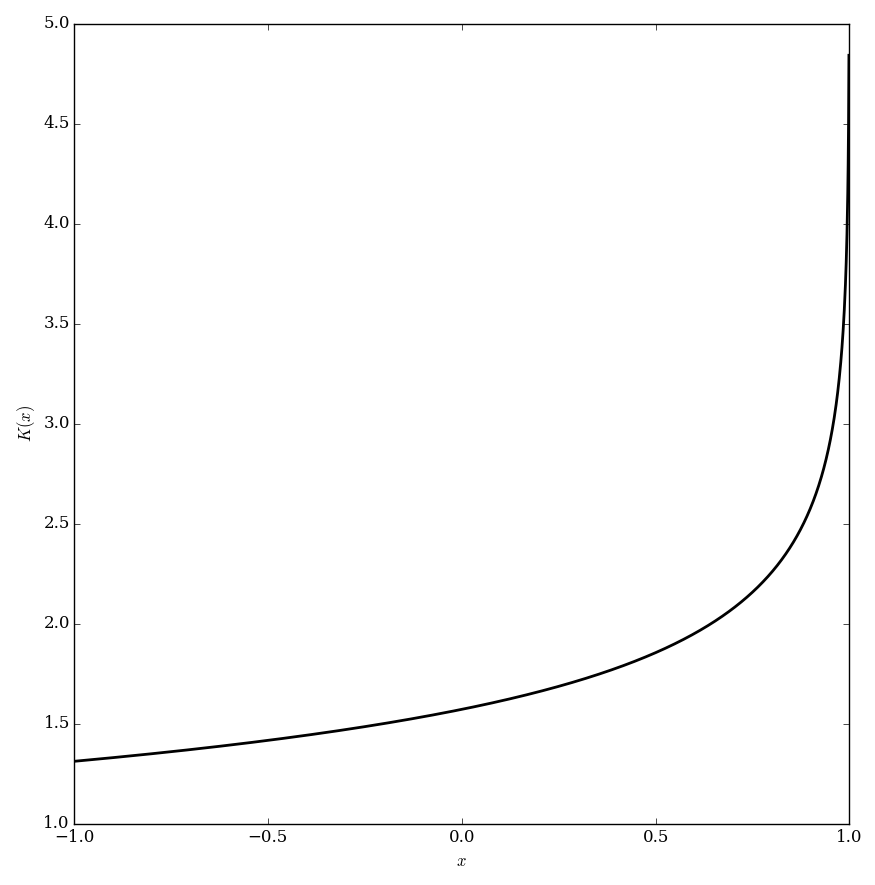
The elliptic $K$ function (also known as the complete elliptic integral of the first kind) is defined by $$K(m)=\displaystyle\int_0^{\frac{\pi}{2}} \dfrac{1}{\sqrt{1-m\sin^2 \theta}} \mathrm{d}\theta.$$
Properties
See Also
Elliptic E
Incomplete Elliptic K
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $17.3.1$