Difference between revisions of "Derivative of arccos"
From specialfunctionswiki
| Line 15: | Line 15: | ||
[[Category:Theorem]] | [[Category:Theorem]] | ||
| + | [[Category:Proven]] | ||
Latest revision as of 07:29, 8 June 2016
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arccos}(z) = -\dfrac{1}{\sqrt{1-z^2}},$$ where $\mathrm{arccos}$ denotes the inverse cosine function.
Proof
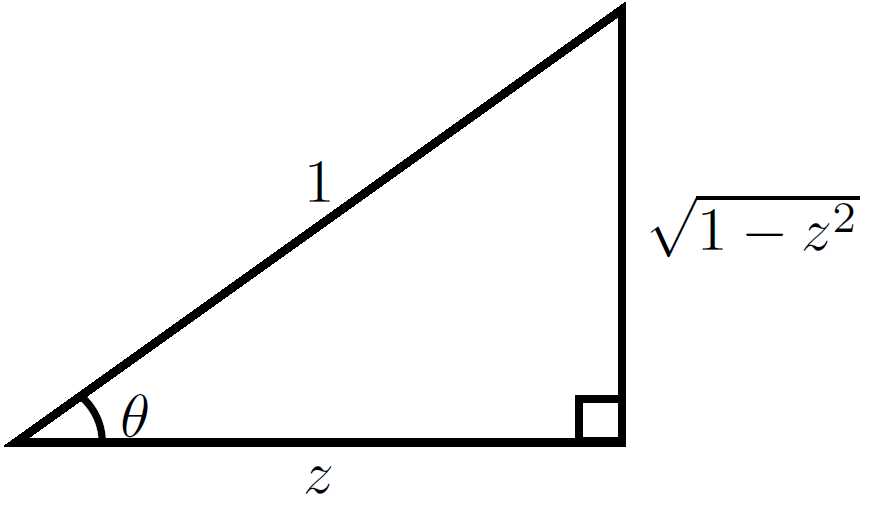
If $\theta=\mathrm{arccos}(z)$ then $\cos(\theta)=z$. Now use implicit differentiation with respect to $z$ to get
$$-\sin(\theta)\theta'=1.$$
The following image shows that $\sin(\mathrm{arccos}(z))=\sqrt{1-z^2}$:
Hence substituting back in $\theta=\mathrm{arccos}(z)$ yields the formula
$$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arccos}(z) = -\dfrac{1}{\sin(\mathrm{arccos}(z))} = -\dfrac{1}{\sqrt{1-z^2}}.█$$