Difference between revisions of "Gamma"
(→See Also) |
|||
| Line 124: | Line 124: | ||
=References= | =References= | ||
| + | * {{BookReference|Higher Transcendental Functions Volume I|1953|Harry Bateman|next=Gamma(z) as integral of a power of log(1/t) for Re(z) greater than 0}}: §1.1 (1) | ||
| + | |||
[http://www.plouffe.fr/simon/math/Artin%20E.%20The%20Gamma%20Function%20%281931%29%2823s%29.pdf The Gamma Function by Emil Artin]<br /> | [http://www.plouffe.fr/simon/math/Artin%20E.%20The%20Gamma%20Function%20%281931%29%2823s%29.pdf The Gamma Function by Emil Artin]<br /> | ||
[http://ocw.mit.edu/courses/mathematics/18-104-seminar-in-analysis-applications-to-number-theory-fall-2006/projects/chan.pdf The sine product formula and the gamma function]<br /> | [http://ocw.mit.edu/courses/mathematics/18-104-seminar-in-analysis-applications-to-number-theory-fall-2006/projects/chan.pdf The sine product formula and the gamma function]<br /> | ||
Revision as of 09:11, 4 June 2016
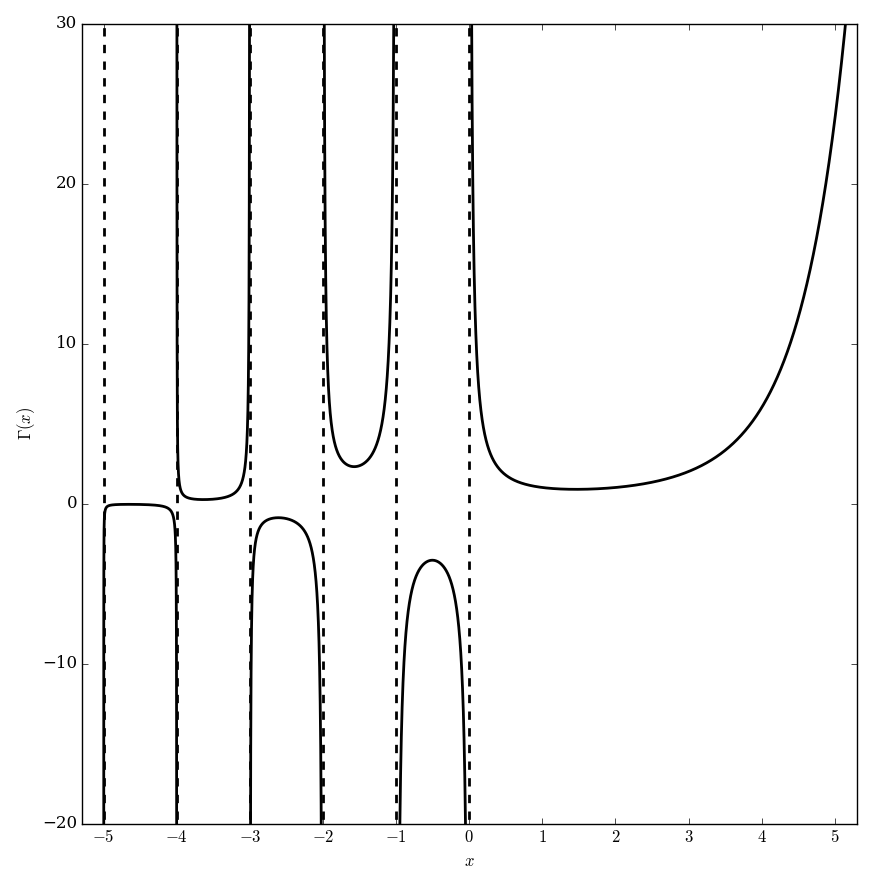
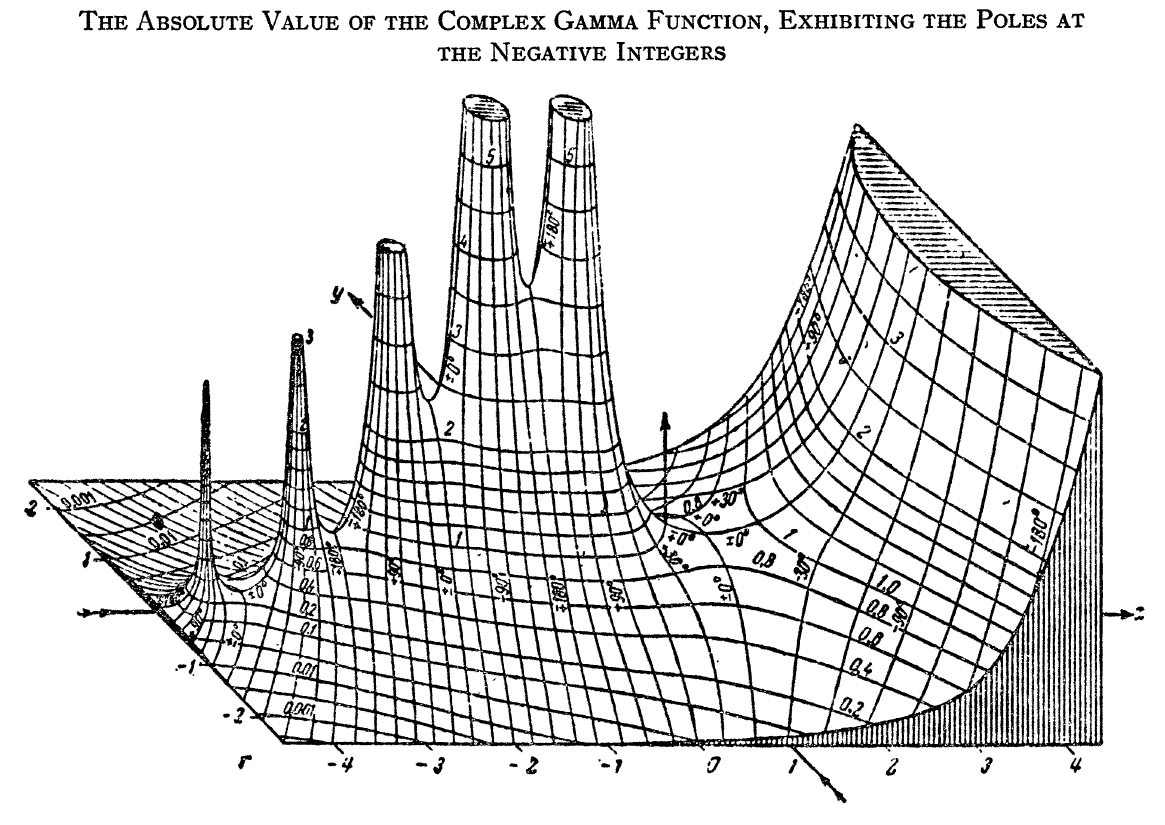
The gamma function is the function defined by the integral (initially for positive values of $x$) by the formula $$\Gamma(x)=\displaystyle\int_0^{\infty} \xi^{x-1}e^{-\xi} \mathrm{d}\xi.$$ The analytic continuation of $\Gamma$ leads to a meromorphic function with poles at the negative integers.
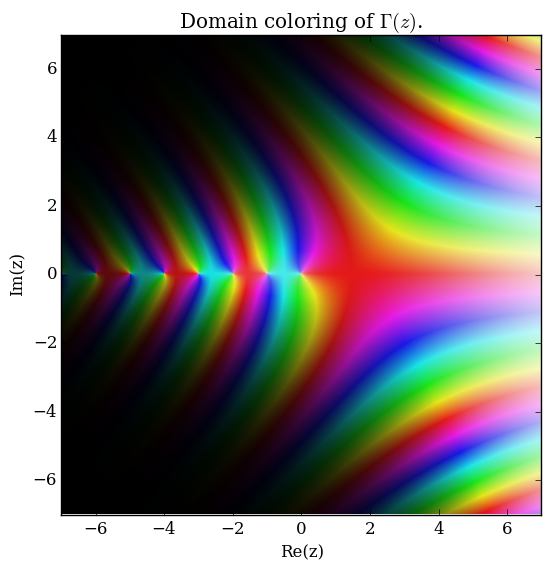
Domain coloring of $\Gamma$.
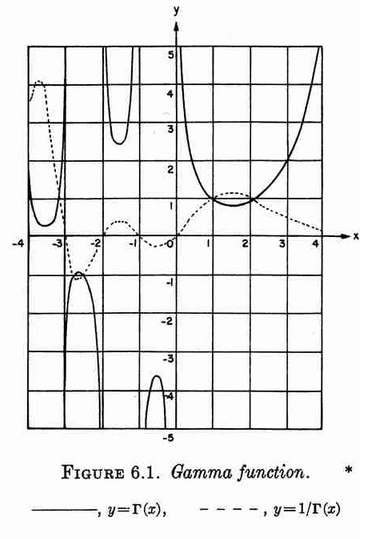
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
Contents
Properties
Theorem
The following formula holds: $$\Gamma(1)=1,$$ where $\Gamma$ denotes the gamma function.
Proof
Compute using the fundamental theorem of calculus, $$\begin{array}{ll} \Gamma(1) &= \displaystyle\int_0^{\infty} \xi^{0} e^{-\xi} \mathrm{d}\xi \\ &= \displaystyle\int_0^{\infty} e^{-\xi} \mathrm{d}\xi \\ &= \left[ -e^{-\xi} \right.\Bigg|_{0}^{\infty} \\ &= 1, \end{array}$$ as was to be shown. █
References
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): Theorem 2.1
Theorem
The following formula holds: $$\Gamma(z+1)=z\Gamma(z),$$ where $\Gamma$ denotes gamma.
Proof
Use integration by parts to compute $$\begin{array}{ll} \Gamma(z+1) &= \displaystyle\int_0^{\infty} \xi^z e^{-\xi} \mathrm{d}\xi \\ &= -\xi^z e^{-\xi}\Bigg|_0^{\infty}- \displaystyle\int_0^{\infty} z \xi^{z-1} e^{-\xi} \mathrm{d}\xi \\ &= z\Gamma(z), \end{array}$$ as was to be shown. █
References
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): Theorem 2.2
- 2010: Roelof Koekoek, Peter A. Lesky and René F. Swarttouw: Hypergeometric Orthogonal Polynomials and Their q-Analogues ... (previous) ... (next): $(1.2.2)$
- 2010: Richard Beals and Roderick Wong: Special functions, a graduate text ... (previous) ... (next): $(2.1.2)$
Theorem
If $n \in \{0,1,2,\ldots\}$, then $$\Gamma(n+1)=n!,$$ where $\Gamma$ denotes the gamma function and $n!$ denotes the factorial of $n$.
Proof
References
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): Theorem 2.3
Proposition: The following formula holds: $$\Gamma(x)=2\displaystyle\int_0^{\infty} e^{-t^2}t^{2x-1}dt.$$
Proof: █
Proposition: The following formula holds: $$\displaystyle\int_0^{\frac{\pi}{2}} \cos^{2x-1}(\theta)\sin^{2y-1}(\theta) d\theta = \dfrac{\Gamma(x)\Gamma(y)}{2\Gamma(x+y)}.$$
Proof: █
Theorem: The following formula holds for $\mathrm{Re}(z)>0$: $$\Gamma(z)=\displaystyle\int_0^1 \log \left( \dfrac{1}{t} \right)^{z-1} dt,$$ where $\Gamma$ denotes the gamma function and $\log$ denotes the logarithm.
Proof: █
Proposition: The following formula holds: $$\Gamma(z)=\lim_{k \rightarrow \infty} \dfrac{k!k^z}{z(z+1)\ldots(z+k)}.$$
Proof: █
Gamma function Weierstrass product
Theorem
The following formula holds: $$\Gamma(s)\zeta(s,a) = \displaystyle\int_0^{\infty} \dfrac{x^{s-1}e^{-ax}}{1-e^{-x}} \mathrm{d}x,$$ where $\Gamma$ denotes the gamma function and $\zeta$ denotes the Hurwitz zeta function.
Proof
References
Proposition: $\Gamma \left( \dfrac{1}{2} \right) = \sqrt{\pi}$.
Proof: █
Corollary: $\displaystyle\int_0^{\infty} e^{-t^2} dt = \dfrac{1}{2}\sqrt{\pi}$.
Theorem (Convexity): The gamma function is logarithmically convex.
Proof: █
Theorem (Legendre Duplication Formula): $$\Gamma(2x)=\dfrac{2^{2x-1}}{\sqrt{\pi}} \Gamma(x)\Gamma \left( x +\dfrac{1}{2} \right).$$
Proof: █
Proposition: If $z=0,-1,-2,\ldots$ then $\Gamma(z)=\infty$.
Proof: █
- REDIRECT Gamma(z)Gamma(1-z)=pi/sin(pi z)
Theorem
The gamma function is the unique function $f$ such that $f(1)=1$, $f(x+1)=xf(x)$ for $x>0$, and $f$ is logarithmically convex.
Proof
References
Theorem: The following formula holds: $$\displaystyle\lim_{t \rightarrow \infty} \dfrac{\Gamma(t+\alpha)}{\Gamma(t)t^{\alpha}}=\displaystyle\lim_{t \rightarrow \infty} \dfrac{\Gamma(t)t^{\alpha}}{\Gamma(t+\alpha)}=1.$$
Proof: proof goes here █
Videos
Gamma Function (playlist)
The Gamma Function: intro (5)
Gamma Integral Function - Introduction
Gamma function
Mod-04 Lec-09 Analytic continuation and the gamma function (Part I)
gamma function - Part 1
Beta Function, Gamma Function and their Properties
What's the Gamma Function?
euler gamma function
Thermodynamics 19 a : Gamma Function 1/2
The Gamma Function: why 0!=1 (5)
Gamma Function Of One-Half: Part 1
Gamma Function Of One-Half: Part 2
Gamma function at 1/2
Contour Integral Definition of the Gamma Function
See Also
Loggamma
Polygamma
Reciprocal gamma
References
- 1953: Harry Bateman: Higher Transcendental Functions Volume I ... (next): §1.1 (1)
The Gamma Function by Emil Artin
The sine product formula and the gamma function
Leonhard Euler's Integral: A Historical Profile of the Gamma Function