Difference between revisions of "Hermite (physicist)"
| Line 1: | Line 1: | ||
| − | The (physicist) Hermite polynomials $H_n$ are a sequence of [[orthogonal polynomials]] with weight function | + | The (physicist) Hermite polynomials $H_n$ are a sequence of [[orthogonal polynomials]] with weight function $w(x)=e^{-x^2}$ over $(-\infty,\infty)$. |
<div align="center"> | <div align="center"> | ||
Revision as of 23:38, 8 July 2016
The (physicist) Hermite polynomials $H_n$ are a sequence of orthogonal polynomials with weight function $w(x)=e^{-x^2}$ over $(-\infty,\infty)$.
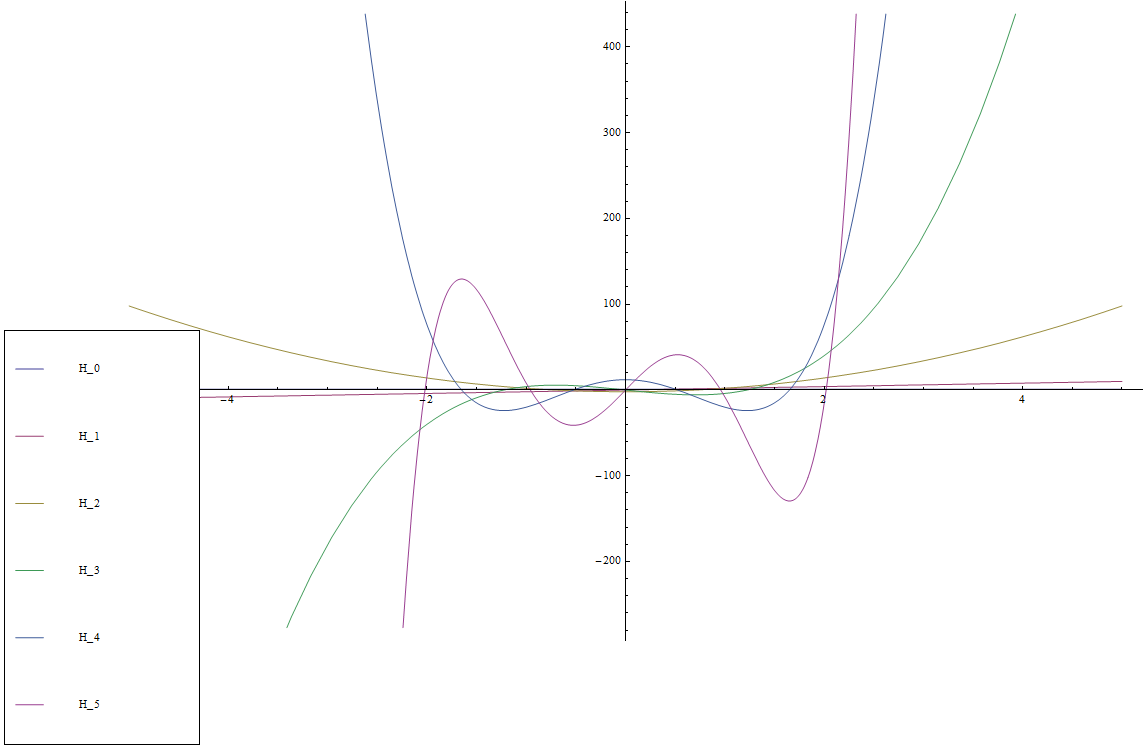
$$\begin{array}{ll} H_0(x)=1\\ H_1(x)=2x\\ H_2(x)=4x^2-2\\ H_3(x)=8x^3-12x\\ H_4(x)=16x^4-48x^2+12\\ H_5(x)=32x^5-160x^3+120x \end{array}$$
Properties
Generating function for Hermite (physicist) polynomials
Closed formula for physicist's Hermite polynomials
Hermite (physicist) polynomial at negative argument
Theorem: (Orthogonality) Let $w(x)=e^{-x^2}$, then $$\displaystyle\int_{-\infty}^{\infty} H_n(x)H_m(x)w(x) dx=\sqrt{\pi}2^nn!\delta_{mn},$$ where $H_n$ denotes the Hermite polynomials and $\delta_{mn}$ denotes the Kronecker delta.
Proof: █
Theorem: The following formula holds: $$H_{n+1}(x)=2xH_n(x)-H_n'(x).$$
Proof: █
Theorem: The following formula holds: $$H_n'(x)=2nH_{n-1}(x).$$
Proof: █
Theorem: The following formula holds: $$H_{n+1}(x)=2xH_n(x)-2nH_{n-1}(x).$$
Proof: █