Difference between revisions of "Takagi function"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| − | Define the function $s(x)=\ | + | Define the function $s(x)=\inf_{n \in \mathbb{Z}} |x-n|$. The Takagi function (also called the blancmange function) is defined by |
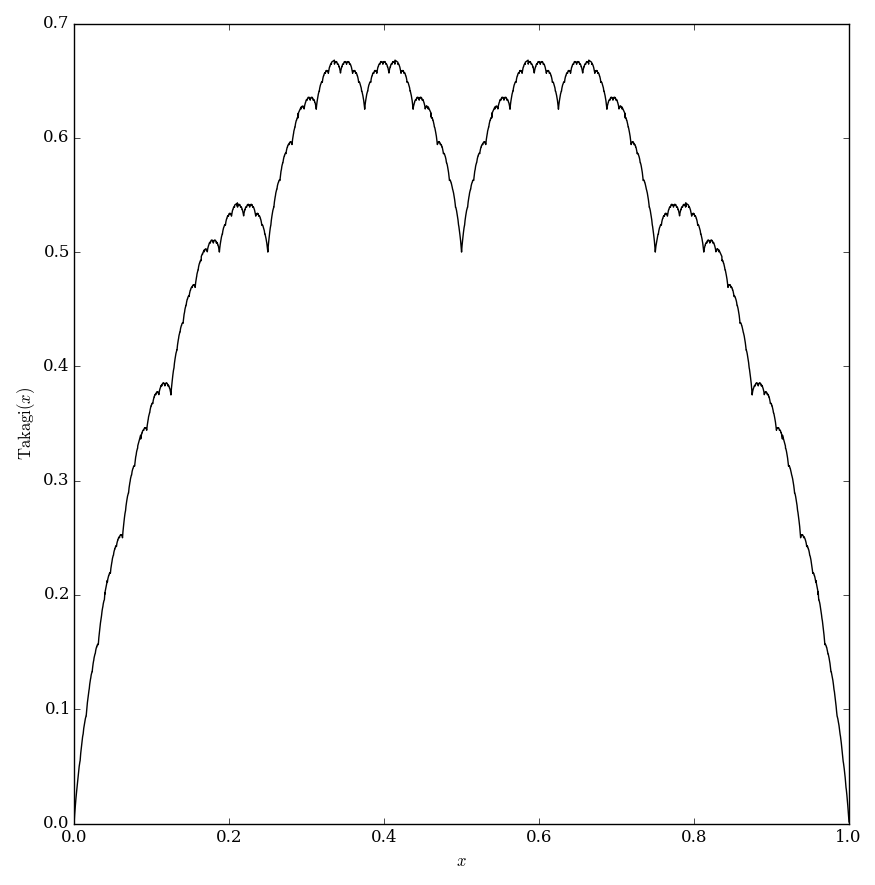
$$\mathrm{takagi}(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{s(2^n x)}{2^n}.$$ | $$\mathrm{takagi}(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{s(2^n x)}{2^n}.$$ | ||
Note: to calculate $s(x)$ you may use $s(x)=\min \left(2^n x - \lfloor 2^n x \rfloor, \lceil 2^n x \rceil - x \right)$, where $\lfloor \cdot \rfloor$ denotes the [[floor]] function and $\lceil \cdot \rceil$ denotes the [[ceiling]] function. | Note: to calculate $s(x)$ you may use $s(x)=\min \left(2^n x - \lfloor 2^n x \rfloor, \lceil 2^n x \rceil - x \right)$, where $\lfloor \cdot \rfloor$ denotes the [[floor]] function and $\lceil \cdot \rceil$ denotes the [[ceiling]] function. | ||
Revision as of 17:26, 22 January 2016
Define the function $s(x)=\inf_{n \in \mathbb{Z}} |x-n|$. The Takagi function (also called the blancmange function) is defined by $$\mathrm{takagi}(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{s(2^n x)}{2^n}.$$ Note: to calculate $s(x)$ you may use $s(x)=\min \left(2^n x - \lfloor 2^n x \rfloor, \lceil 2^n x \rceil - x \right)$, where $\lfloor \cdot \rfloor$ denotes the floor function and $\lceil \cdot \rceil$ denotes the ceiling function.
Graph of $\mathrm{takagi}$ on $[0,1]$.
Properties
Theorem: The Takagi function is continuous on $\mathbb{R}$.
Proof: █
Theorem: The Takagi function is nowhere differentiable on $\mathbb{R}$.
Proof: █
