Difference between revisions of "Kelvin ber"
From specialfunctionswiki
| Line 13: | Line 13: | ||
<center>{{:Kelvin functions footer}}</center> | <center>{{:Kelvin functions footer}}</center> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:37, 24 May 2016
The $\mathrm{ber}_{\nu}$ function is defined as $$\mathrm{ber}_{\nu}(z)=\mathrm{Re} \hspace{2pt} J_{\nu} \left( z e^{\frac{3\pi i}{4}} \right),$$ where $\mathrm{Re}$ denotes the real part of a complex number and $J_{\nu}$ denotes the Bessel function of the first kind.
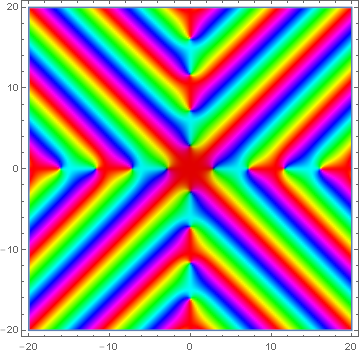
Domain coloring of $\mathrm{ber}_0$.