Difference between revisions of "Sine"
From specialfunctionswiki
(→Properties) |
(→Properties) |
||
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| − | [[Derivative of sine]] | + | [[Derivative of sine]]<br /> |
| − | [[Pythagorean identity for sin and cos]] | + | [[Pythagorean identity for sin and cos]]<br /> |
| − | [[Taylor series of sine]] | + | [[Taylor series of sine]]<br /> |
| − | [[Weierstrass factorization of sine]] | + | [[Weierstrass factorization of sine]]<br /> |
| − | [[Gamma-Sine_Relation]] | + | [[Gamma-Sine_Relation]]<br /> |
| − | [[Beta in terms of sine and cosine]] | + | [[Beta in terms of sine and cosine]]<br /> |
| − | [[Relationship between sine and hypergeometric 0F1]] | + | [[Relationship between sine and hypergeometric 0F1]]<br /> |
| − | [[Relationship between spherical Bessel j sub nu and sine]] | + | [[Relationship between spherical Bessel j sub nu and sine]]<br /> |
| − | [[Relationship between sin and sinh]] | + | [[Relationship between sin and sinh]]<br /> |
| − | [[Relationship between sinh and sin]] | + | [[Relationship between sinh and sin]]<br /> |
| − | [[Relationship between sine, Gudermannian, and tanh]] | + | [[Relationship between sine, Gudermannian, and tanh]]<br /> |
| − | [[Relationship between tanh, inverse Gudermannian, and sin]] | + | [[Relationship between tanh, inverse Gudermannian, and sin]]<br /> |
=See Also= | =See Also= | ||
Revision as of 00:26, 4 June 2016
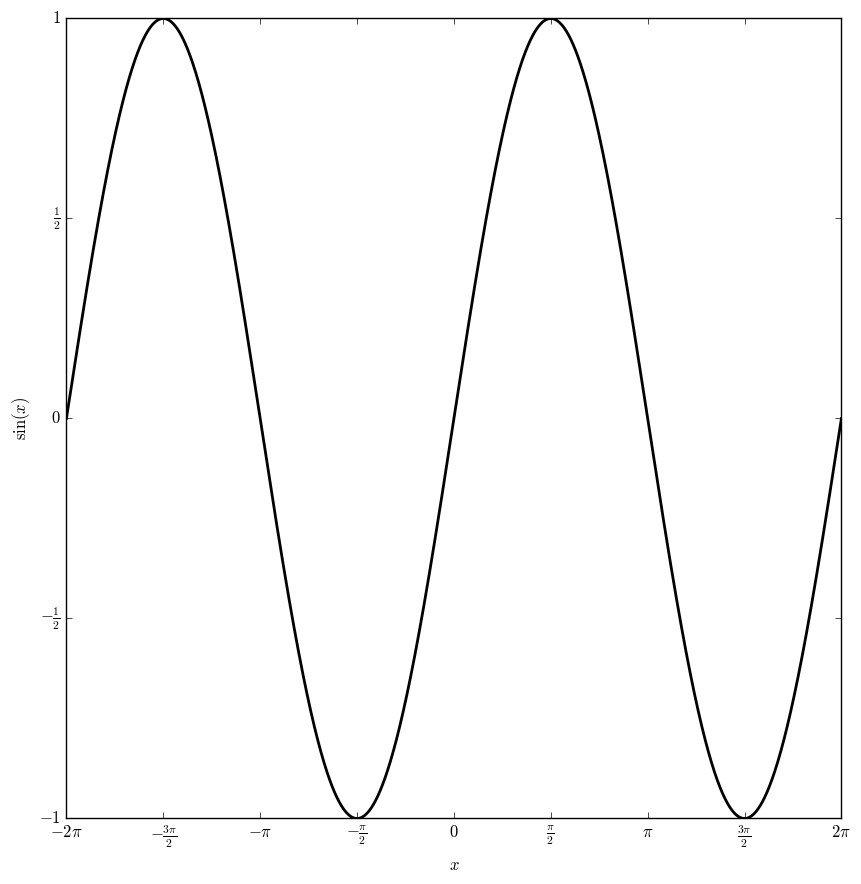
The sine function $\sin \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by $$\sin(z)=\dfrac{e^{iz}-e^{-iz}}{2i},$$ where $e^z$ is the exponential function.
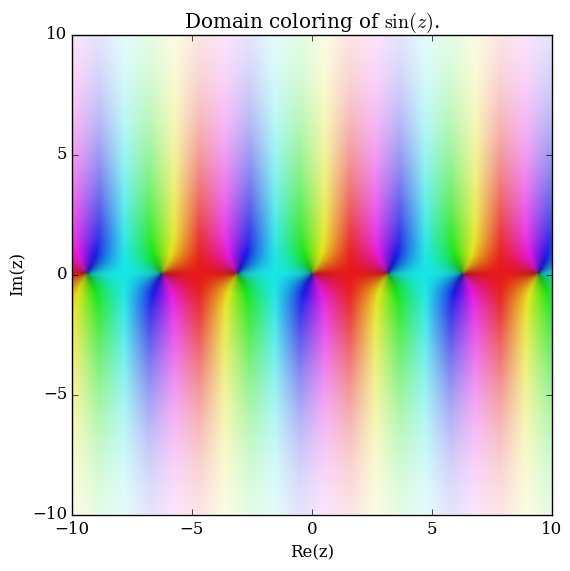
Domain coloring of $\sin$.
Contents
Properties
Derivative of sine
Pythagorean identity for sin and cos
Taylor series of sine
Weierstrass factorization of sine
Gamma-Sine_Relation
Beta in terms of sine and cosine
Relationship between sine and hypergeometric 0F1
Relationship between spherical Bessel j sub nu and sine
Relationship between sin and sinh
Relationship between sinh and sin
Relationship between sine, Gudermannian, and tanh
Relationship between tanh, inverse Gudermannian, and sin
See Also
Videos
References
The sine product formula and the gamma function