Difference between revisions of "Cosine"
From specialfunctionswiki
(→Properties) |
(→Properties) |
||
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| − | [[Derivative of cosine]] | + | [[Derivative of cosine]]<br /> |
| − | [[Taylor series of cosine]] | + | [[Taylor series of cosine]]<br /> |
| − | [[Weierstrass factorization of cosine]] | + | [[Weierstrass factorization of cosine]]<br /> |
| − | [[Beta in terms of sine and cosine]] | + | [[Beta in terms of sine and cosine]]<br /> |
| − | [[Relationship between cosine and hypergeometric 0F1]] | + | [[Relationship between cosine and hypergeometric 0F1]]<br /> |
| − | [[Relationship between spherical Bessel y sub nu and cosine]] | + | [[Relationship between spherical Bessel y sub nu and cosine]]<br /> |
| − | [[Relationship between cosh and cos]] | + | [[Relationship between cosh and cos]]<br /> |
| − | [[Relationship between cos and cosh]] | + | [[Relationship between cos and cosh]]<br /> |
| − | [[Relationship between cosine, Gudermannian, and sech]] | + | [[Relationship between cosine, Gudermannian, and sech]]<br /> |
| − | [[Relationship between sech, inverse Gudermannian, and cos]] | + | [[Relationship between sech, inverse Gudermannian, and cos]]<br /> |
=See Also= | =See Also= | ||
Revision as of 00:43, 4 June 2016
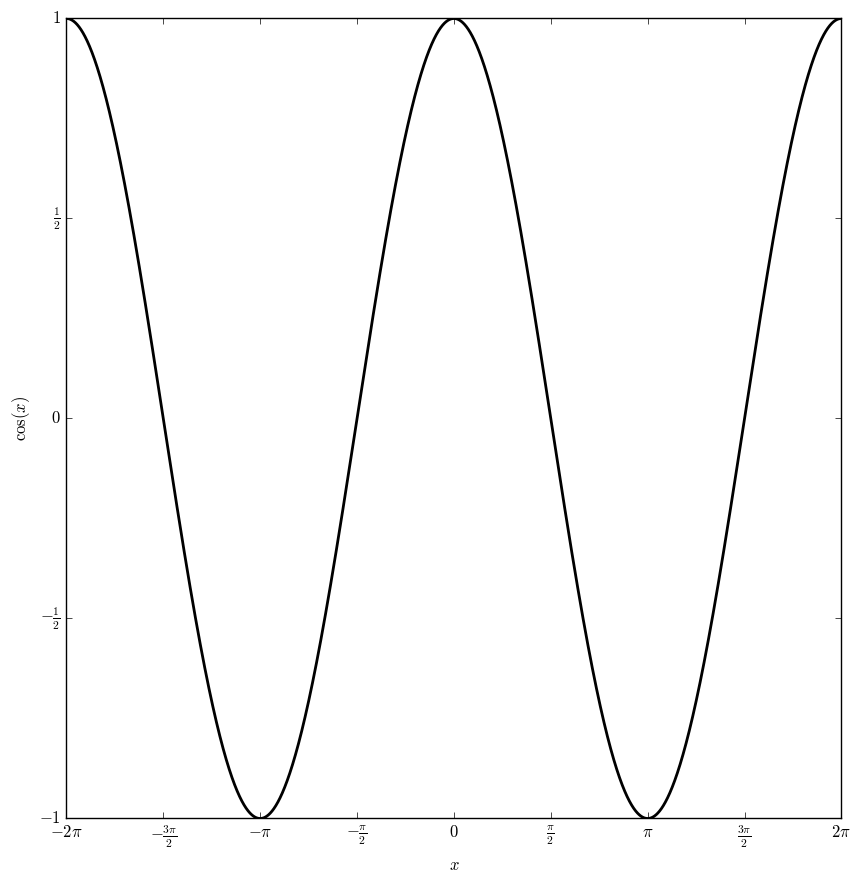
The cosine function, $\cos \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula $$\cos(z)=\dfrac{e^{iz}+e^{-iz}}{2},$$ where $e^z$ is the exponential function.
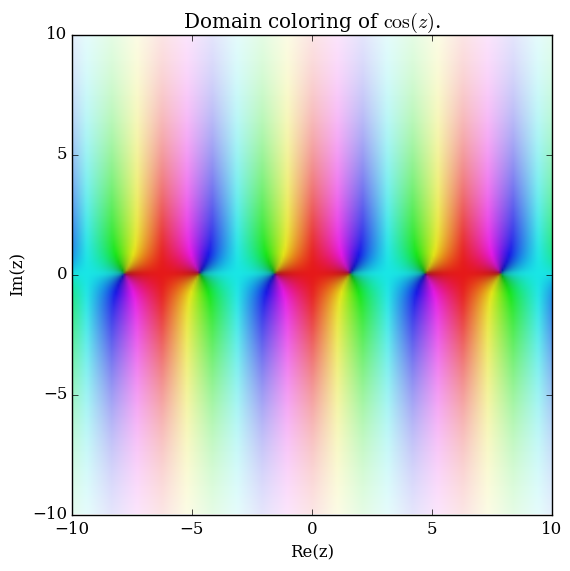
Domain coloring of $\cos$.
Properties
Derivative of cosine
Taylor series of cosine
Weierstrass factorization of cosine
Beta in terms of sine and cosine
Relationship between cosine and hypergeometric 0F1
Relationship between spherical Bessel y sub nu and cosine
Relationship between cosh and cos
Relationship between cos and cosh
Relationship between cosine, Gudermannian, and sech
Relationship between sech, inverse Gudermannian, and cos