Difference between revisions of "Chebyshev psi function"
From specialfunctionswiki
(Created page with "The Chebyshev $\psi$ function is $$\psi(x) = \displaystyle\sum_{p^k \leq x} \log p = \displaystyle\sum_{n \leq x} \Lambda(n),$$ where $\Lambda$ denotes the Mangoldt functio...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
$$\psi(x) = \displaystyle\sum_{p^k \leq x} \log p = \displaystyle\sum_{n \leq x} \Lambda(n),$$ | $$\psi(x) = \displaystyle\sum_{p^k \leq x} \log p = \displaystyle\sum_{n \leq x} \Lambda(n),$$ | ||
where $\Lambda$ denotes the [[Mangoldt function]]. | where $\Lambda$ denotes the [[Mangoldt function]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
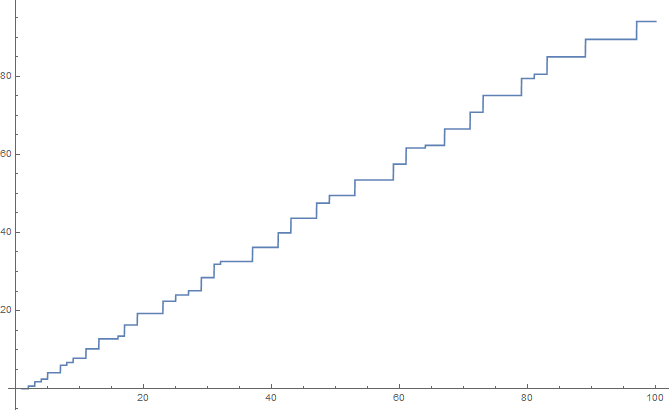
| + | File:Chebyshevpsiplotto100.png|Plot of $\psi$ on $[0,100]$. | ||
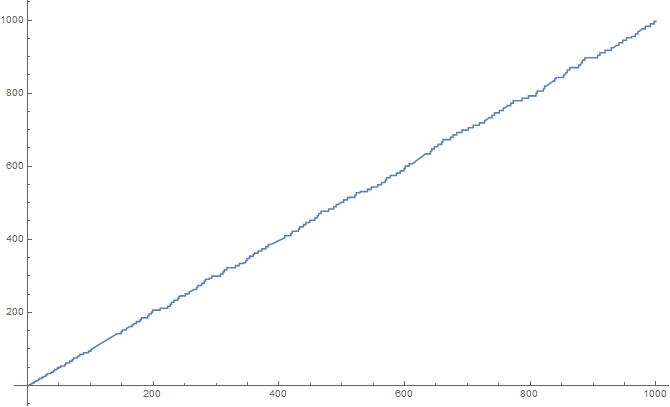
| + | File:Chebyshevpsiplotto1000.png|Plot of $\psi$ on $[0,1000]$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | {{:Number theory functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 03:47, 22 June 2016
The Chebyshev $\psi$ function is $$\psi(x) = \displaystyle\sum_{p^k \leq x} \log p = \displaystyle\sum_{n \leq x} \Lambda(n),$$ where $\Lambda$ denotes the Mangoldt function.