Difference between revisions of "Kelvin bei"
From specialfunctionswiki
| Line 11: | Line 11: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| − | + | ||
| + | =Properties= | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|Higher Transcendental Functions Volume II|1953|Harry Bateman|prev=Kelvin ber|next=findme}}: $\S 7.2.3 (19)$ | ||
{{:Kelvin functions footer}} | {{:Kelvin functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 22:17, 8 July 2016
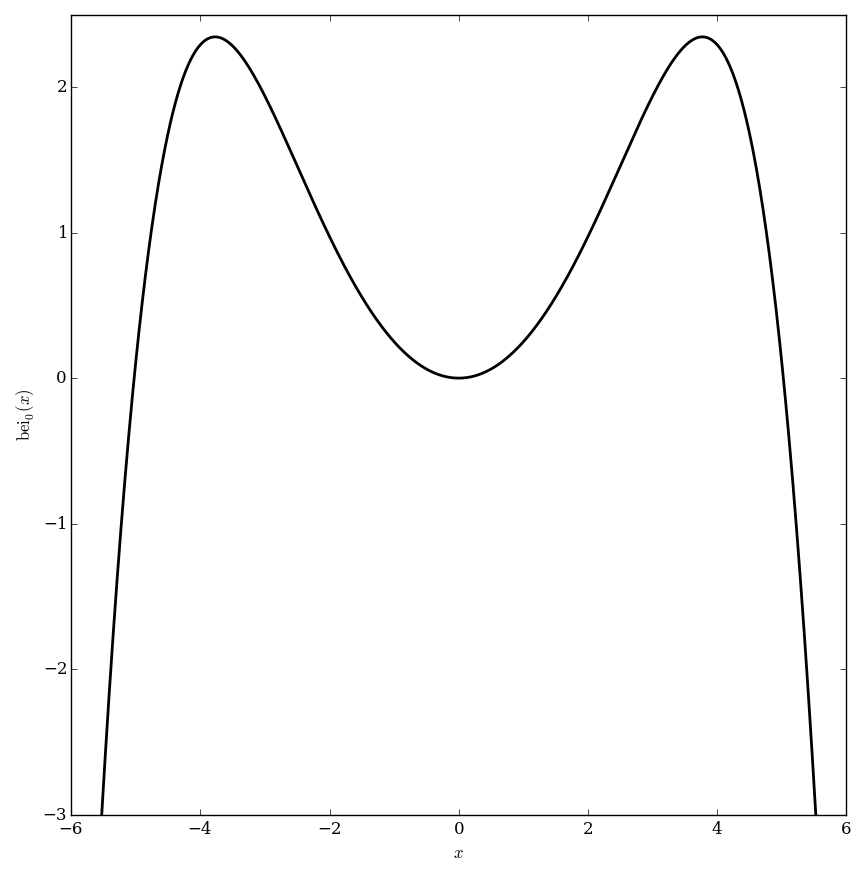
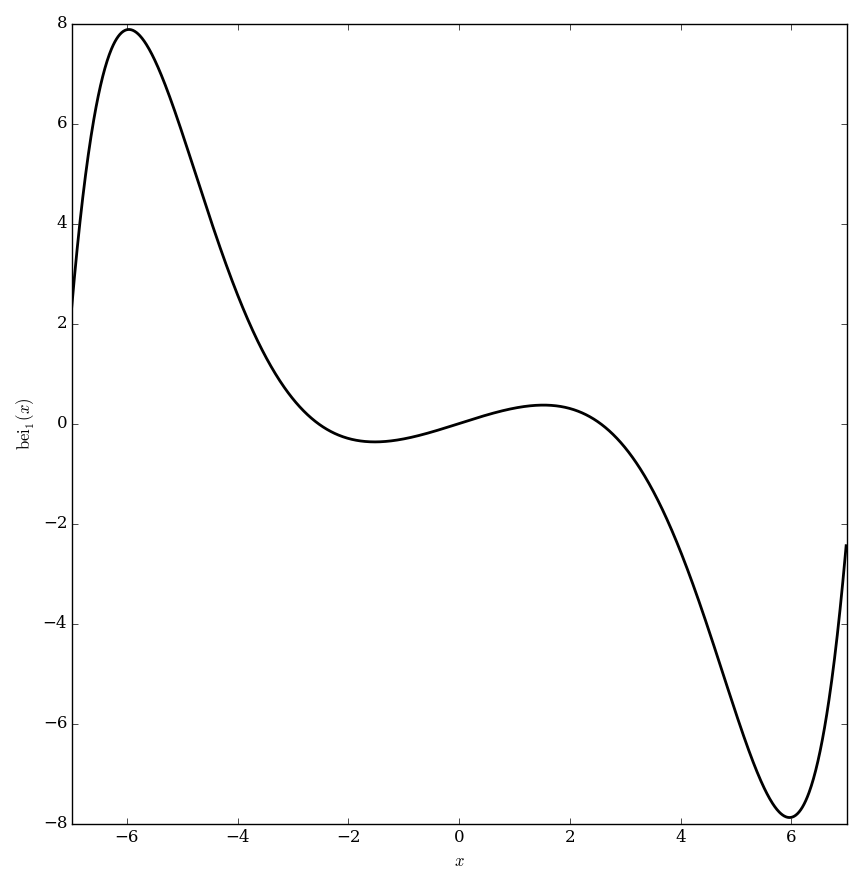
The $\mathrm{bei}_{\nu}$ function is defined as $$\mathrm{bei}_{\nu}(z)=\mathrm{Im} \hspace{2pt} J_{\nu} \left( z e^{\frac{3\pi i}{4}} \right),$$ where $\mathrm{Im}$ denotes the imaginary part of a complex number and $J_{\nu}$ denotes the Bessel function of the first kind.
Graph of $\mathrm{bei}_0$.
Graph of $\mathrm{bei}_1$.
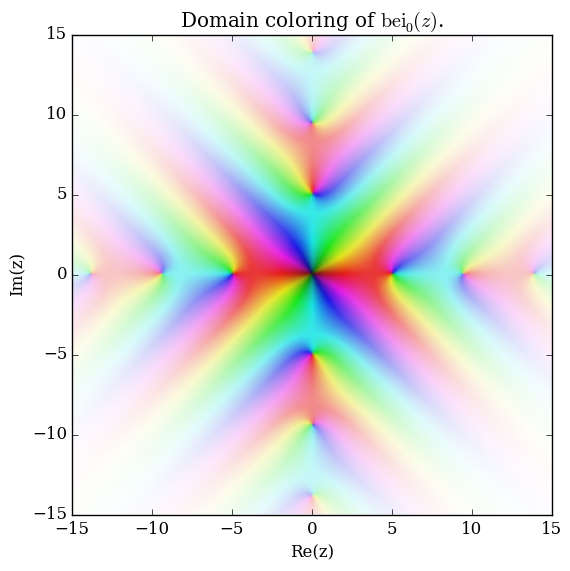
Domain coloring of $\mathrm{bei}_0$.
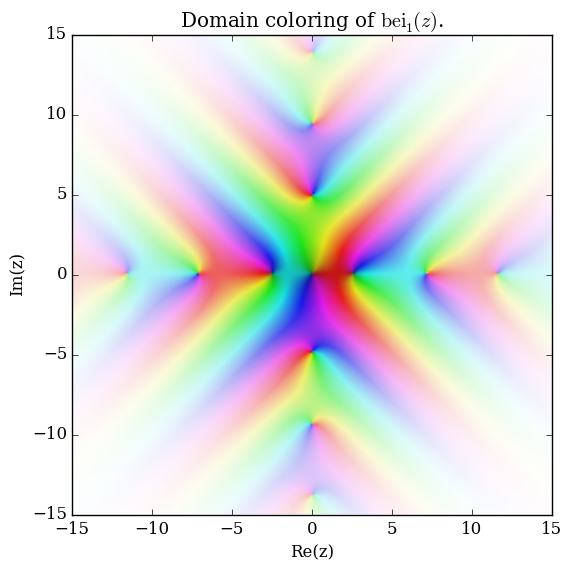
Domain coloring of $\mathrm{bei}_1$.
Properties
References
- 1953: Harry Bateman: Higher Transcendental Functions Volume II ... (previous) ... (next): $\S 7.2.3 (19)$
