Difference between revisions of "Sech"
From specialfunctionswiki
(Created page with "500px") |
(→Properties) |
||
| (18 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File: | + | __NOTOC__ |
| + | The hyperbolic secant function $\mathrm{sech} \colon \mathbb{R} \rightarrow (0,1]$ is defined by | ||
| + | $$\mathrm{sech}(z)=\dfrac{1}{\cosh(z)},$$ | ||
| + | where $\cosh(z)$ denotes the [[cosh|hyperbolic cosine]]. Since this function is not [[one-to-one]], we define the [[arcsech|inverse hyperbolic secant function]] as the [[inverse function]] of $\mathrm{sech}$ restricted to $[0,\infty)$. | ||
| + | <div align="center"> | ||
| + | <gallery> | ||
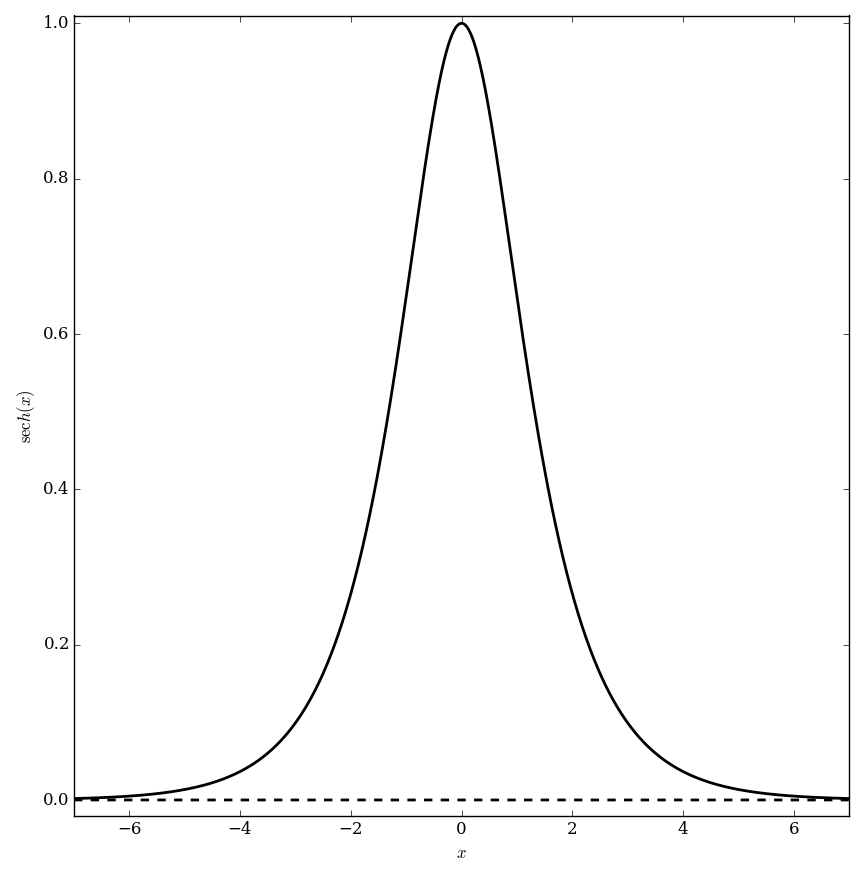
| + | File:Sechplot.png|Graph of $\mathrm{sech}$ on $[-5,5]$. | ||
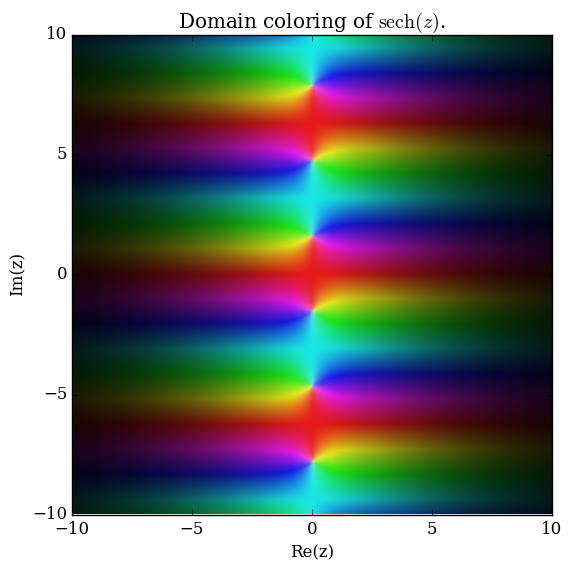
| + | File:Complexsechplot.png|[[Domain coloring]] of [[analytic continuation]] of $\mathrm{sech}$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Derivative of sech]]<br /> | ||
| + | [[Antiderivative of sech]]<br /> | ||
| + | [[Relationship between cosine, Gudermannian, and sech]]<br /> | ||
| + | [[Relationship between sech, inverse Gudermannian, and cos]]<br /> | ||
| + | [[Pythagorean identity for tanh and sech]]<br /> | ||
| + | |||
| + | =See Also= | ||
| + | [[Arcsech]] | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Csch|next=Coth}}: $4.5.5$ | ||
| + | |||
| + | {{:Hyperbolic trigonometric functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 23:35, 21 October 2017
The hyperbolic secant function $\mathrm{sech} \colon \mathbb{R} \rightarrow (0,1]$ is defined by $$\mathrm{sech}(z)=\dfrac{1}{\cosh(z)},$$ where $\cosh(z)$ denotes the hyperbolic cosine. Since this function is not one-to-one, we define the inverse hyperbolic secant function as the inverse function of $\mathrm{sech}$ restricted to $[0,\infty)$.
Domain coloring of analytic continuation of $\mathrm{sech}$.
Properties
Derivative of sech
Antiderivative of sech
Relationship between cosine, Gudermannian, and sech
Relationship between sech, inverse Gudermannian, and cos
Pythagorean identity for tanh and sech
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.5$