Difference between revisions of "Sech"
From specialfunctionswiki
(→Properties) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 15: | Line 15: | ||
[[Relationship between cosine, Gudermannian, and sech]]<br /> | [[Relationship between cosine, Gudermannian, and sech]]<br /> | ||
[[Relationship between sech, inverse Gudermannian, and cos]]<br /> | [[Relationship between sech, inverse Gudermannian, and cos]]<br /> | ||
| + | [[Pythagorean identity for tanh and sech]]<br /> | ||
=See Also= | =See Also= | ||
| Line 20: | Line 21: | ||
=References= | =References= | ||
| − | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Csch|next=Coth}}: 4.5.5 | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Csch|next=Coth}}: $4.5.5$ |
{{:Hyperbolic trigonometric functions footer}} | {{:Hyperbolic trigonometric functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 23:35, 21 October 2017
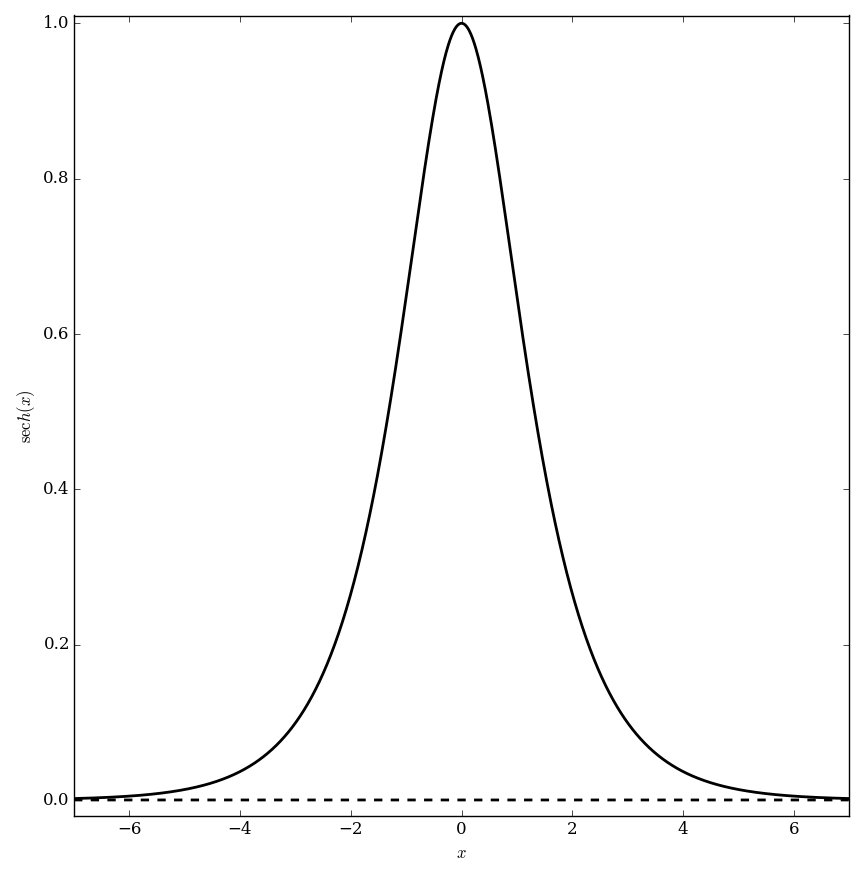
The hyperbolic secant function $\mathrm{sech} \colon \mathbb{R} \rightarrow (0,1]$ is defined by $$\mathrm{sech}(z)=\dfrac{1}{\cosh(z)},$$ where $\cosh(z)$ denotes the hyperbolic cosine. Since this function is not one-to-one, we define the inverse hyperbolic secant function as the inverse function of $\mathrm{sech}$ restricted to $[0,\infty)$.
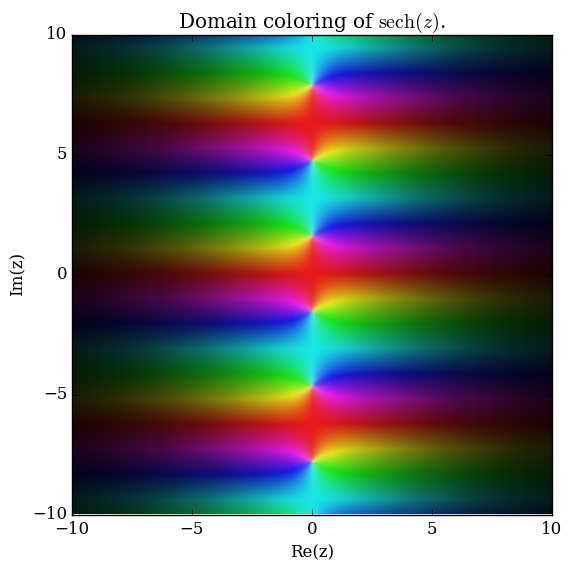
Domain coloring of analytic continuation of $\mathrm{sech}$.
Properties
Derivative of sech
Antiderivative of sech
Relationship between cosine, Gudermannian, and sech
Relationship between sech, inverse Gudermannian, and cos
Pythagorean identity for tanh and sech
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.5$