Difference between revisions of "Struve function"
From specialfunctionswiki
| Line 1: | Line 1: | ||
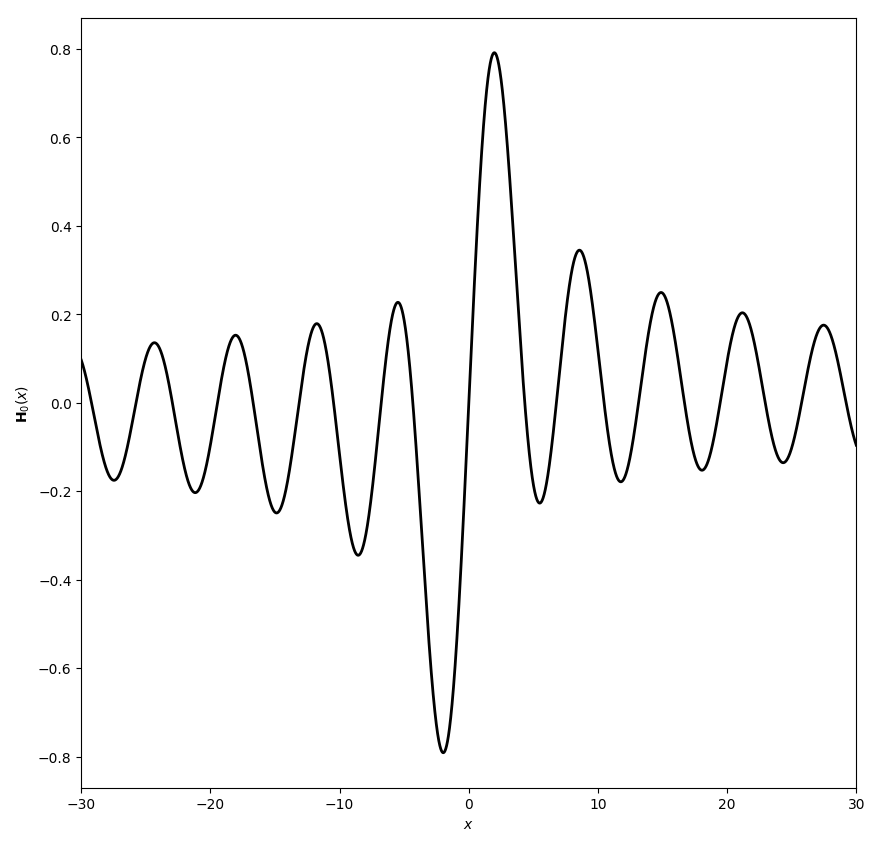
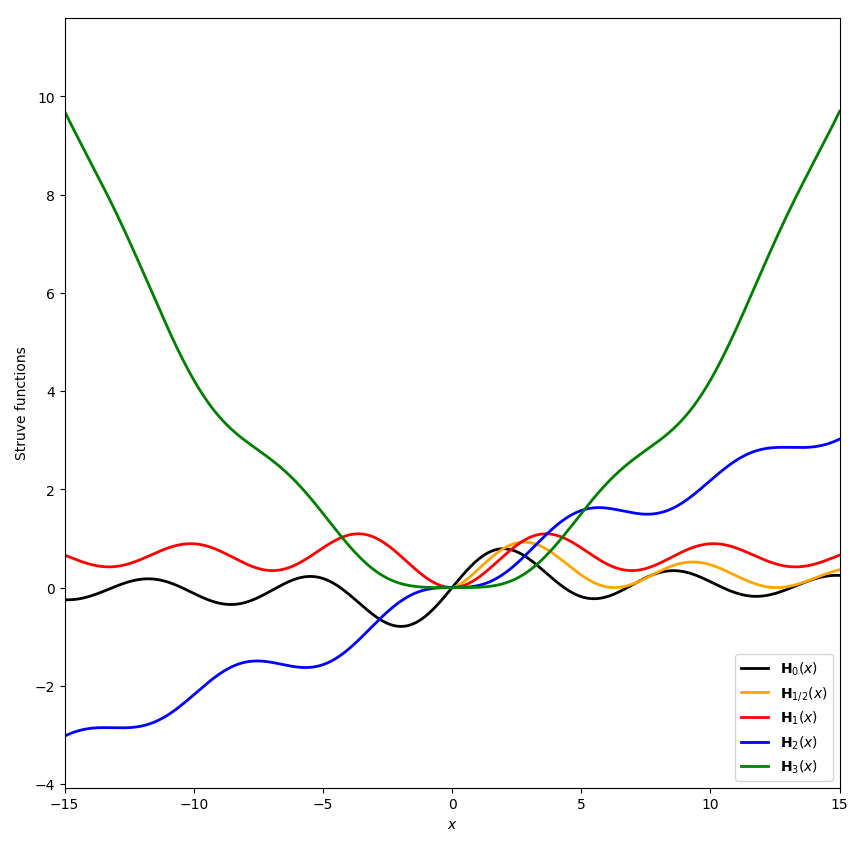
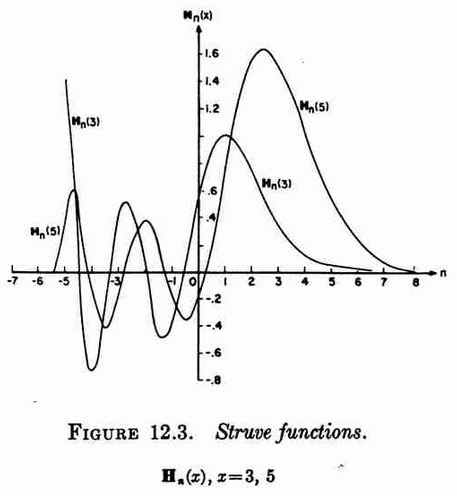
The Struve functions are defined by | The Struve functions are defined by | ||
| − | $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma(k+\nu+\frac{3}{2})}.$$ | + | $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma \left(k+\nu+\frac{3}{2} \right)}.$$ |
<div align="center"> | <div align="center"> | ||
| Line 17: | Line 17: | ||
=References= | =References= | ||
| − | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Struve H0}}: $12.1.3$ | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 22:40, 31 October 2017
The Struve functions are defined by $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma \left(k+\nu+\frac{3}{2} \right)}.$$
Properties
Relationship between Struve function and hypergeometric pFq
Relationship between Weber function 0 and Struve function 0
Relationship between Weber function 1 and Struve function 1
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $12.1.3$