Difference between revisions of "Euler totient"
(→Videos) |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Euler's totient function $\phi$ (not to be confused with the [[Euler phi]]) is defined | + | __NOTOC__ |
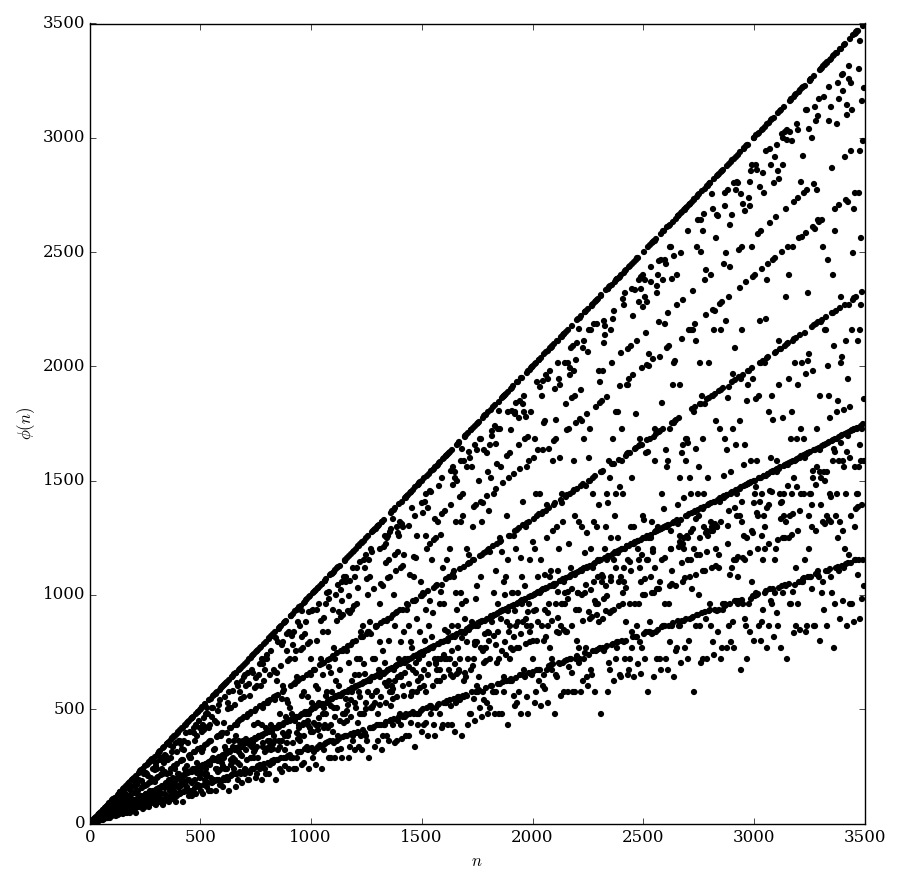
| + | Euler's totient function $\phi \colon \{1,2,3,\ldots\} \rightarrow \{1,2,3,\ldots\}$ (not to be confused with the [[Euler phi]]) is defined so that $\phi(n)$ equals the number of positive integers less than or equal to $n$ that are [[relatively prime]] to $n$. | ||
<div align="center"> | <div align="center"> | ||
| Line 15: | Line 16: | ||
=Videos= | =Videos= | ||
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=QbsWEVcjJy0 Euler's Phi Function] (6 October 2010)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=ATPiEJIT1FI Euler's Totient Function] (14 October 2011)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=4hu6Z8ZCl5Q Euler Totient Theorem, Fermat Little Theorems] (19 December 2011)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=fjhefD0NrH8 Möbius and Euler totient functions] (2 September 2012)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=IBJuVHGRfLg Prime Factorisation and Euler Totient Function Part 14] (16 April 2014)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=o8NrDpaIfVk Application of Euler Totient Function Part 16] (17 April 2014)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=GZbdmCIhmpA Euler's Totient Function: what it is and how it works] (4 July 2014)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=9Pox0bIgC8g Euler's Totient Theorem: What is Euler's Totient Theorem and Why is it useful?] (6 July 2014)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=F7a6XfxCjbE Euler's Totient Function | How To Find Totient Of A Number Using Euler's Product Formula] (7 July 2014)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=ygfjHZAb0p8 03 Modern cryptography 08 Euler's totient function] (23 September 2014)<br /> |
| − | [https://www.youtube.com/watch?v= | + | [https://www.youtube.com/watch?v=njaJpmBK7QI Euler's totient function] (8 January 2015)<br /> |
| + | [https://www.youtube.com/watch?v=-NOSYaHh2nE Euler Totient (phi) Function Examples (Part 1)] (27 November 2016)<br /> | ||
| + | [https://www.youtube.com/watch?v=EcAT1XmHouk Euler totient function made easy] (17 December 2017)<br /> | ||
=References= | =References= | ||
Latest revision as of 01:58, 21 December 2017
Euler's totient function $\phi \colon \{1,2,3,\ldots\} \rightarrow \{1,2,3,\ldots\}$ (not to be confused with the Euler phi) is defined so that $\phi(n)$ equals the number of positive integers less than or equal to $n$ that are relatively prime to $n$.
Properties
Sum of totient equals zeta(z-1)/zeta(z) for Re(z) greater than 2
Sum of totient equals z/((1-z) squared)
Product representation of totient
Euler totient is multiplicative
Videos
Euler's Phi Function (6 October 2010)
Euler's Totient Function (14 October 2011)
Euler Totient Theorem, Fermat Little Theorems (19 December 2011)
Möbius and Euler totient functions (2 September 2012)
Prime Factorisation and Euler Totient Function Part 14 (16 April 2014)
Application of Euler Totient Function Part 16 (17 April 2014)
Euler's Totient Function: what it is and how it works (4 July 2014)
Euler's Totient Theorem: What is Euler's Totient Theorem and Why is it useful? (6 July 2014)
Euler's Totient Function | How To Find Totient Of A Number Using Euler's Product Formula (7 July 2014)
03 Modern cryptography 08 Euler's totient function (23 September 2014)
Euler's totient function (8 January 2015)
Euler Totient (phi) Function Examples (Part 1) (27 November 2016)
Euler totient function made easy (17 December 2017)
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $24.3.2 \mathrm{I}.A.$