Difference between revisions of "Prime counting"
From specialfunctionswiki
(→Properties) |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The prime counting function $\pi \colon \mathbb{R} \rightarrow \mathbb{Z}^+$ is defined by the formula | The prime counting function $\pi \colon \mathbb{R} \rightarrow \mathbb{Z}^+$ is defined by the formula | ||
$$\pi(x) = \{\mathrm{number \hspace{2pt} of \hspace{2pt} primes} \leq x \}.$$ | $$\pi(x) = \{\mathrm{number \hspace{2pt} of \hspace{2pt} primes} \leq x \}.$$ | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
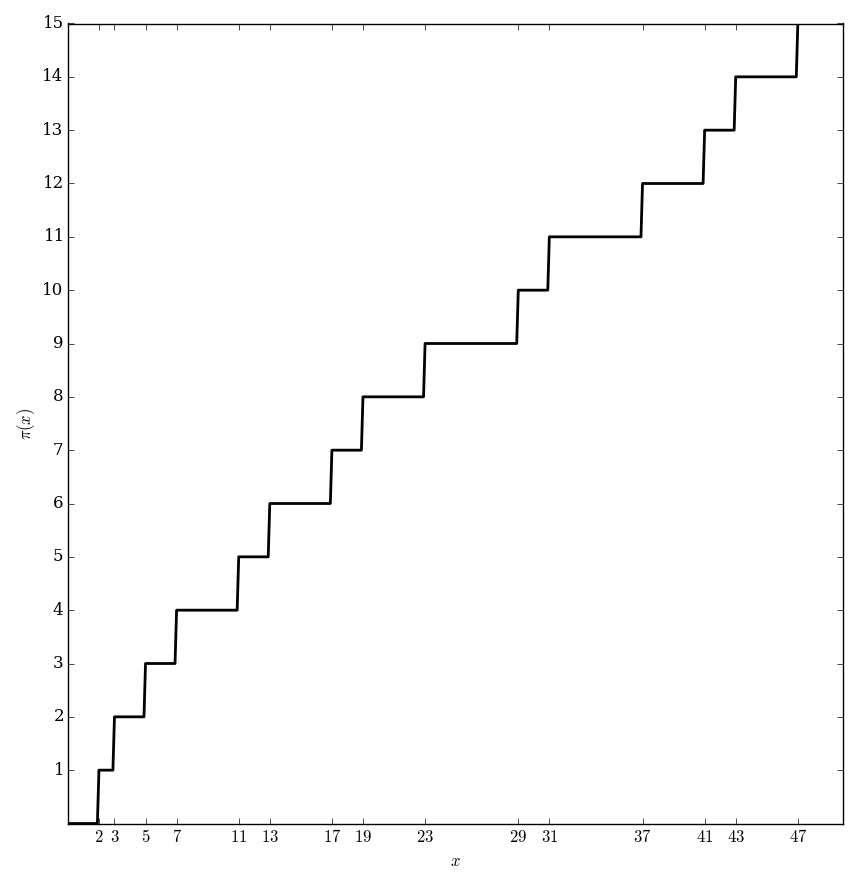
| + | File:Primecountingplot.png|Graph of $\pi(x)$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| − | + | [[Prime number theorem, pi and x/log(x)]]<br /> | |
| − | + | [[Prime number theorem, logarithmic integral]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
=References= | =References= | ||
[http://people.mpim-bonn.mpg.de/zagier/files/doi/10.2307/2975232/fulltext.pdf Newman's short proof of the prime number theorem] | [http://people.mpim-bonn.mpg.de/zagier/files/doi/10.2307/2975232/fulltext.pdf Newman's short proof of the prime number theorem] | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
| + | |||
| + | {{:Number theory functions footer}} | ||
Latest revision as of 06:35, 22 June 2016
The prime counting function $\pi \colon \mathbb{R} \rightarrow \mathbb{Z}^+$ is defined by the formula $$\pi(x) = \{\mathrm{number \hspace{2pt} of \hspace{2pt} primes} \leq x \}.$$
Properties
Prime number theorem, pi and x/log(x)
Prime number theorem, logarithmic integral
References
Newman's short proof of the prime number theorem