Difference between revisions of "Riemann-Siegel Z"
From specialfunctionswiki
| Line 9: | Line 9: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 18:30, 24 May 2016
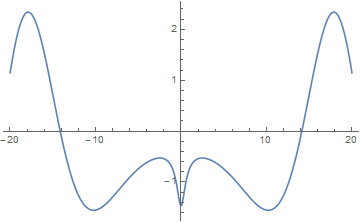
The Riemann-Siegel $Z$ function is defined by $$Z(t)=e^{i\theta(t)}\zeta \left( \dfrac{1}{2}+it \right),$$ where $\theta$ denotes the Riemann-Siegel theta function and $\zeta$ denotes the Riemann zeta function.
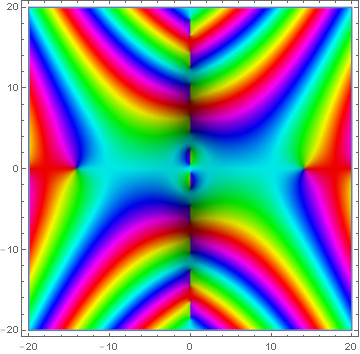
Domain coloring of analytic continuation of $Z(t)$.