Difference between revisions of "Sine"
From specialfunctionswiki
| (20 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The sine function $\sin \colon \mathbb{ | + | __NOTOC__ |
| + | The sine function $\sin \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by | ||
| + | $$\sin(z)=\dfrac{e^{iz}-e^{-iz}}{2i},$$ | ||
| + | where $e^{iz}$ denotes the [[exponential]]. | ||
<div align="center"> | <div align="center"> | ||
| Line 5: | Line 8: | ||
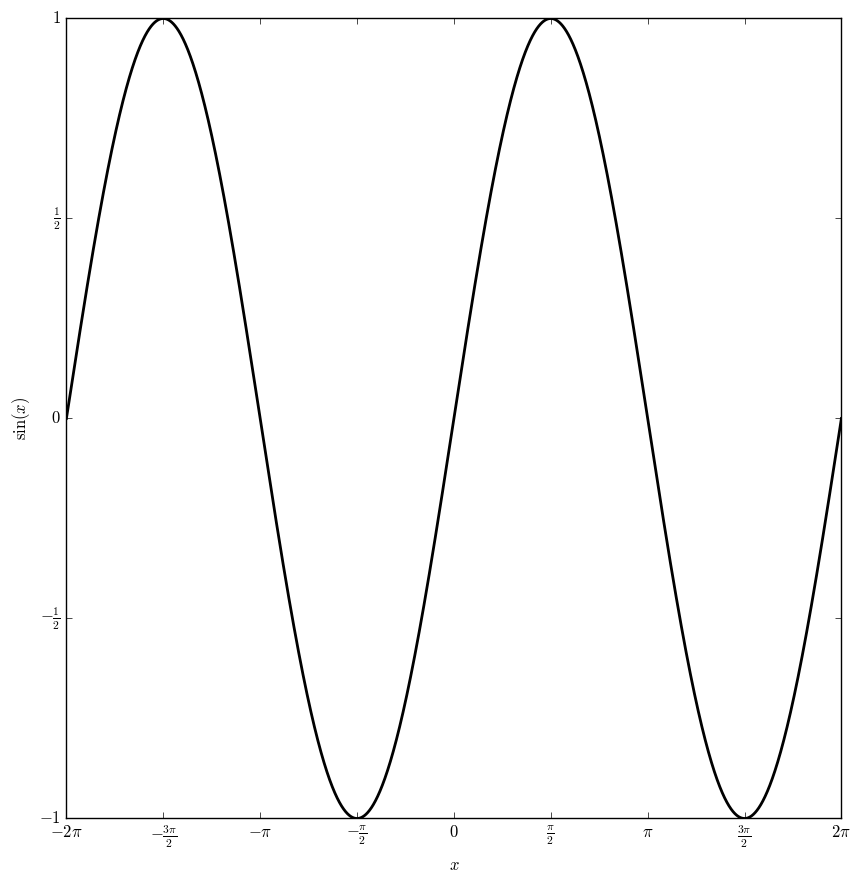
File:Sineplot.png|Graph of $\sin$ on $[-2\pi,2\pi]$. | File:Sineplot.png|Graph of $\sin$ on $[-2\pi,2\pi]$. | ||
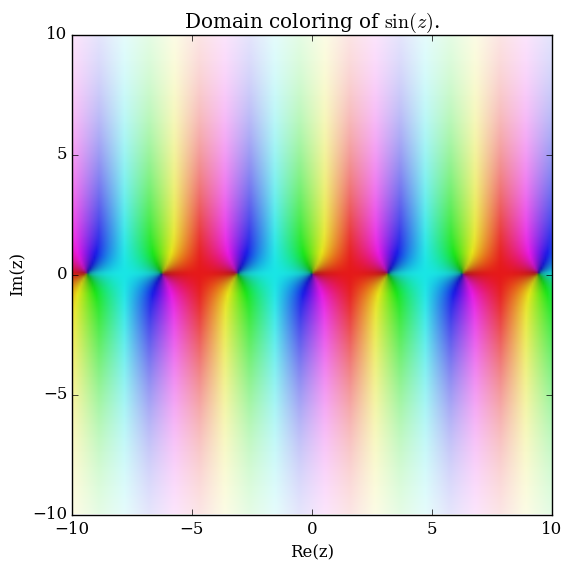
File:Complexsineplot.png|[[Domain coloring]] of $\sin$. | File:Complexsineplot.png|[[Domain coloring]] of $\sin$. | ||
| + | File:Trig Functions Diagram.svg|Trigonometric functions diagram using the unit circle. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of sine]]<br /> | |
| − | + | [[Pythagorean identity for sin and cos]]<br /> | |
| − | + | [[Taylor series of sine]]<br /> | |
| − | + | [[Weierstrass factorization of sine]]<br /> | |
| − | + | [[Euler's reflection formula for gamma]]<br /> | |
| − | + | [[Beta in terms of sine and cosine]]<br /> | |
| − | + | [[Relationship between sine and hypergeometric 0F1]]<br /> | |
| − | + | [[Relationship between spherical Bessel j sub nu and sine]]<br /> | |
| − | + | [[Relationship between sin and sinh]]<br /> | |
| − | + | [[Relationship between sinh and sin]]<br /> | |
| − | + | [[Relationship between sine, Gudermannian, and tanh]]<br /> | |
| − | + | [[Relationship between tanh, inverse Gudermannian, and sin]]<br /> | |
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=WD-n26cAFm0] | ||
=See Also= | =See Also= | ||
[[Arcsin]] <br /> | [[Arcsin]] <br /> | ||
| + | [[Arcsinh]] <br /> | ||
| + | [[Cosecant]]<br /> | ||
[[Sinh]] <br /> | [[Sinh]] <br /> | ||
| − | |||
| − | = | + | =External links= |
| − | [ | + | [http://ocw.mit.edu/courses/mathematics/18-104-seminar-in-analysis-applications-to-number-theory-fall-2006/projects/chan.pdf The sine product formula and the gamma function]<br /> |
=References= | =References= | ||
| − | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Cosine}}: $4.3.1$ | |
| + | |||
| + | {{:Trigonometric functions footer}} | ||
| − | + | [[Category:SpecialFunction]] | |
| + | [[Category:Definition]] | ||
Latest revision as of 17:34, 1 July 2017
The sine function $\sin \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by $$\sin(z)=\dfrac{e^{iz}-e^{-iz}}{2i},$$ where $e^{iz}$ denotes the exponential.
Graph of $\sin$ on $[-2\pi,2\pi]$.
Domain coloring of $\sin$.
Trigonometric functions diagram using the unit circle.
Properties
Derivative of sine
Pythagorean identity for sin and cos
Taylor series of sine
Weierstrass factorization of sine
Euler's reflection formula for gamma
Beta in terms of sine and cosine
Relationship between sine and hypergeometric 0F1
Relationship between spherical Bessel j sub nu and sine
Relationship between sin and sinh
Relationship between sinh and sin
Relationship between sine, Gudermannian, and tanh
Relationship between tanh, inverse Gudermannian, and sin
Videos
See Also
External links
The sine product formula and the gamma function
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.3.1$
