Difference between revisions of "Tangent"
From specialfunctionswiki
| (8 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
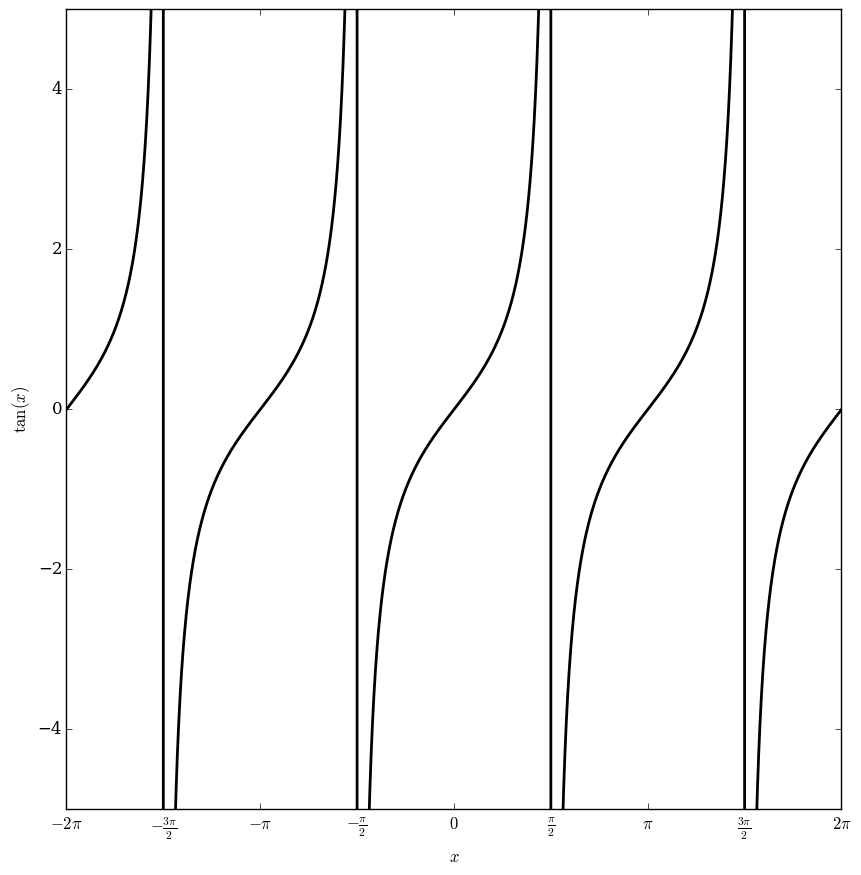
| − | File: | + | File:Tangentplot.png|Graph of $\tan$ over $[-2\pi,2\pi]$. |
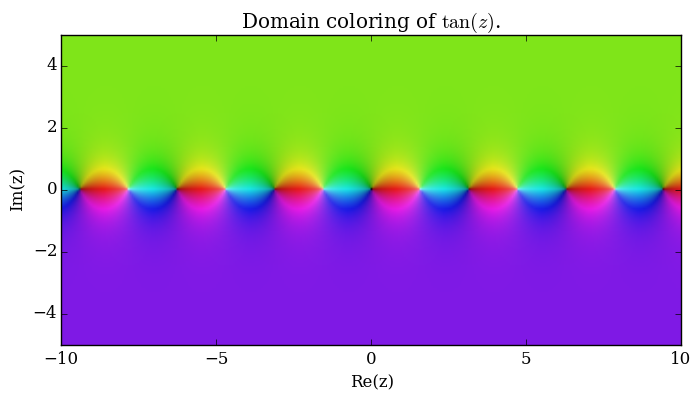
File:Complextangentplot.png|[[Domain coloring]] of $\tan$. | File:Complextangentplot.png|[[Domain coloring]] of $\tan$. | ||
| + | File:Trig Functions Diagram.svg|Trig functions diagram using the unit circle. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of tangent]]<br /> | |
| − | + | [[Relationship between tan and tanh]]<br /> | |
| − | + | [[Relationship between tanh and tan]]<br /> | |
| − | + | [[Relationship between tangent, Gudermannian, and sinh]]<br /> | |
| − | + | [[Relationship between sinh, inverse Gudermannian, and tan]]<br /> | |
=See Also= | =See Also= | ||
| Line 21: | Line 22: | ||
[[Arctanh]] <br /> | [[Arctanh]] <br /> | ||
| − | + | =References= | |
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Cosine|next=Cosecant}}: 4.3.3 | ||
| + | |||
| + | {{:Trigonometric functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 03:38, 6 July 2016
The tangent function is defined as the ratio of the sine and cosine functions: $$\tan(z) = \dfrac{\sin(z)}{\cos(z)}.$$
Graph of $\tan$ over $[-2\pi,2\pi]$.
Domain coloring of $\tan$.
Trig functions diagram using the unit circle.
Properties
Derivative of tangent
Relationship between tan and tanh
Relationship between tanh and tan
Relationship between tangent, Gudermannian, and sinh
Relationship between sinh, inverse Gudermannian, and tan
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.3.3
