Difference between revisions of "Modified Bessel K"
From specialfunctionswiki
m (Tom moved page Modified Bessel K sub nu to Modified Bessel K) |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
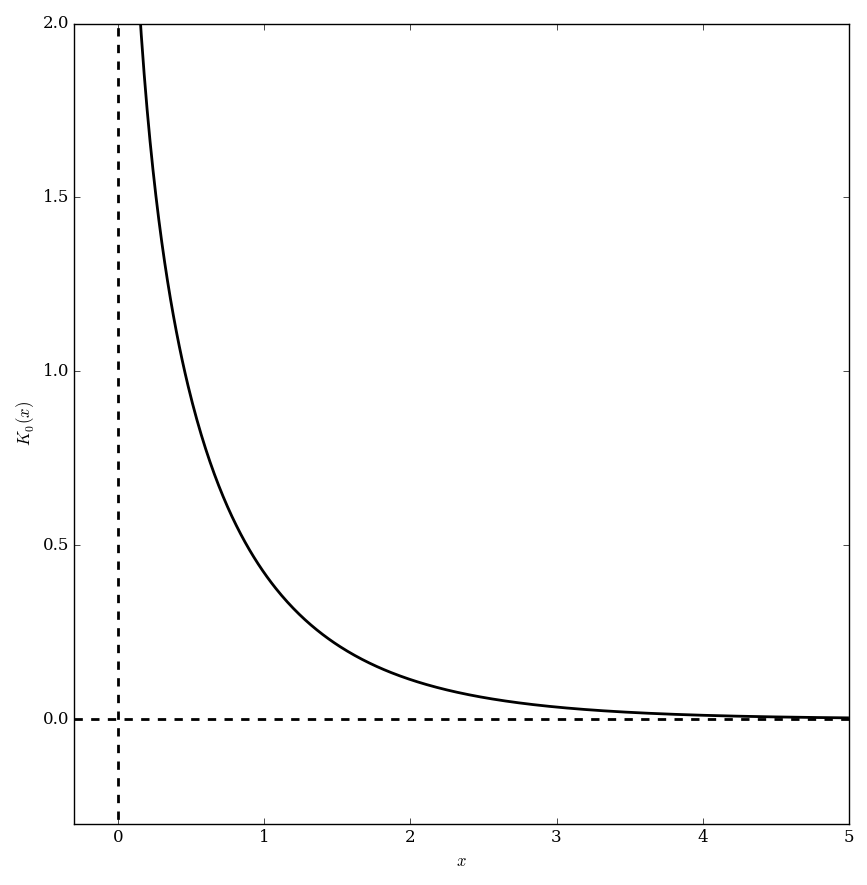
| − | File:Domaincoloringbesselksub1.png|[[Domain coloring]] of $K_1 | + | File:Besselk,n=0plot.png|Graph of $K_0$. |
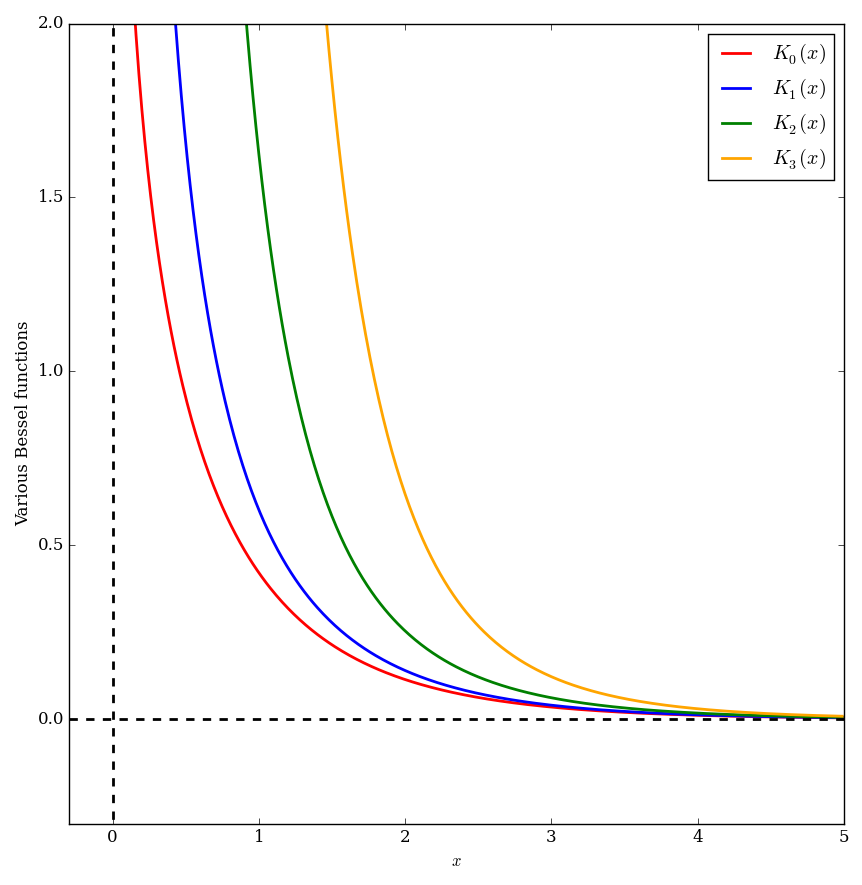
| + | File:Multiplebesselkplot.png|Graphs of $K_0$, $K_1$, $K_2$, and $K_3$. | ||
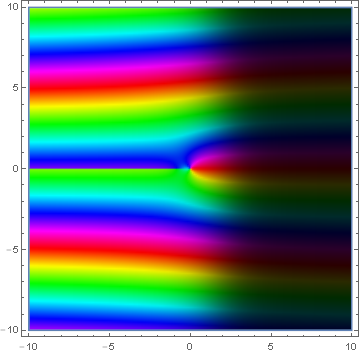
| + | File:Domaincoloringbesselksub1.png|[[Domain coloring]] of $K_1$. | ||
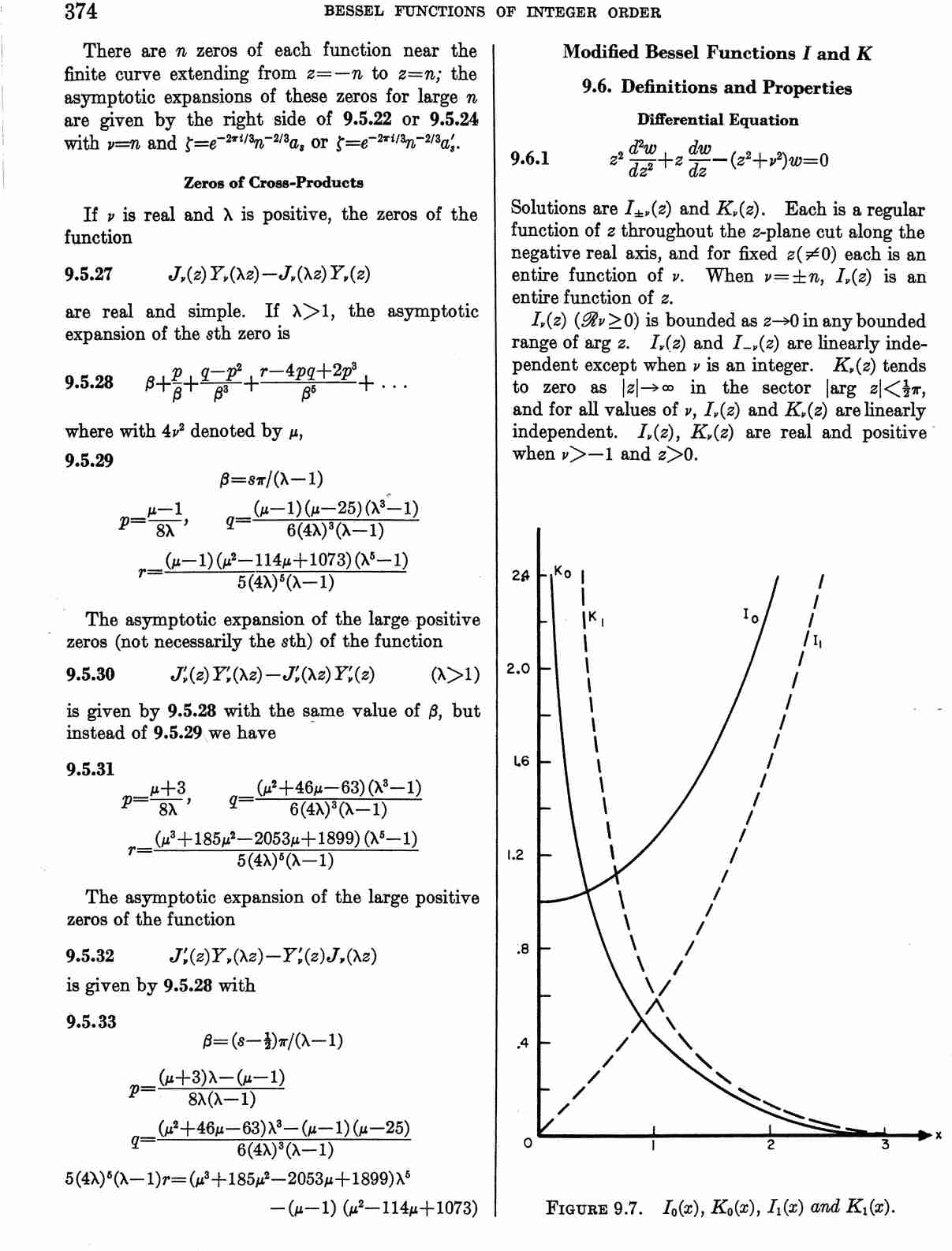
File:Page 374 (Abramowitz&Stegun).jpg|Modified Bessel functions from Abramowitz&Stegun. | File:Page 374 (Abramowitz&Stegun).jpg|Modified Bessel functions from Abramowitz&Stegun. | ||
</gallery> | </gallery> | ||
| Line 12: | Line 14: | ||
=Properties= | =Properties= | ||
| − | + | [[Relationship between Airy Ai and modified Bessel K]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | =References= | |
| + | [http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/page_374.htm] | ||
| − | + | [[Category:SpecialFunction]] | |
| − | + | {{:Bessel functions footer}} | |
| − | |||
Latest revision as of 23:46, 10 June 2016
The modified Bessel function of the second kind is defined by $$K_{\nu}(z)=\dfrac{\pi}{2} \dfrac{I_{-\nu}(z)-I_{\nu}(z)}{\sin(\nu \pi)},$$ where $I_{\nu}$ is the modified Bessel function of the first kind.
Graph of $K_0$.
Graphs of $K_0$, $K_1$, $K_2$, and $K_3$.
Domain coloring of $K_1$.
Modified Bessel functions from Abramowitz&Stegun.
.jpg)
Properties
Relationship between Airy Ai and modified Bessel K
