Difference between revisions of "Coth"
From specialfunctionswiki
(→Properties) |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
The hyperbolic cotangent is defined by | The hyperbolic cotangent is defined by | ||
| − | $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)},$$ | + | $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)}=\dfrac{\mathrm{cosh}(z)}{\mathrm{sinh}(z)},$$ |
where $\tanh$ denotes the [[Tanh|hyperbolic tangent]] function. | where $\tanh$ denotes the [[Tanh|hyperbolic tangent]] function. | ||
| Line 18: | Line 19: | ||
[[Relationship between csc, Gudermannian, and coth]]<br /> | [[Relationship between csc, Gudermannian, and coth]]<br /> | ||
[[Relationship between coth, inverse Gudermannian, and csc]]<br /> | [[Relationship between coth, inverse Gudermannian, and csc]]<br /> | ||
| + | [[Pythagorean identity for coth and csch]]<br /> | ||
| + | [[Coth of a sum]]<br /> | ||
| + | [[z coth(z) = 2z/(e^(2z)-1) + z]]<br /> | ||
| + | [[z coth(z) = sum of 2^(2n)B_(2n) z^(2n)/(2n)!]]<br /> | ||
| + | [[z coth(z) = 2 Sum of (-1)^(n+1) zeta(2n) z^(2n)/pi^(2n)]]<br /> | ||
=Videos= | =Videos= | ||
| Line 25: | Line 31: | ||
[[Arccoth]] | [[Arccoth]] | ||
| − | + | =References= | |
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Sech|next=Relationship between sinh and sin}}: $4.5.6$ | ||
| + | |||
| + | {{:Hyperbolic trigonometric functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 05:53, 4 March 2018
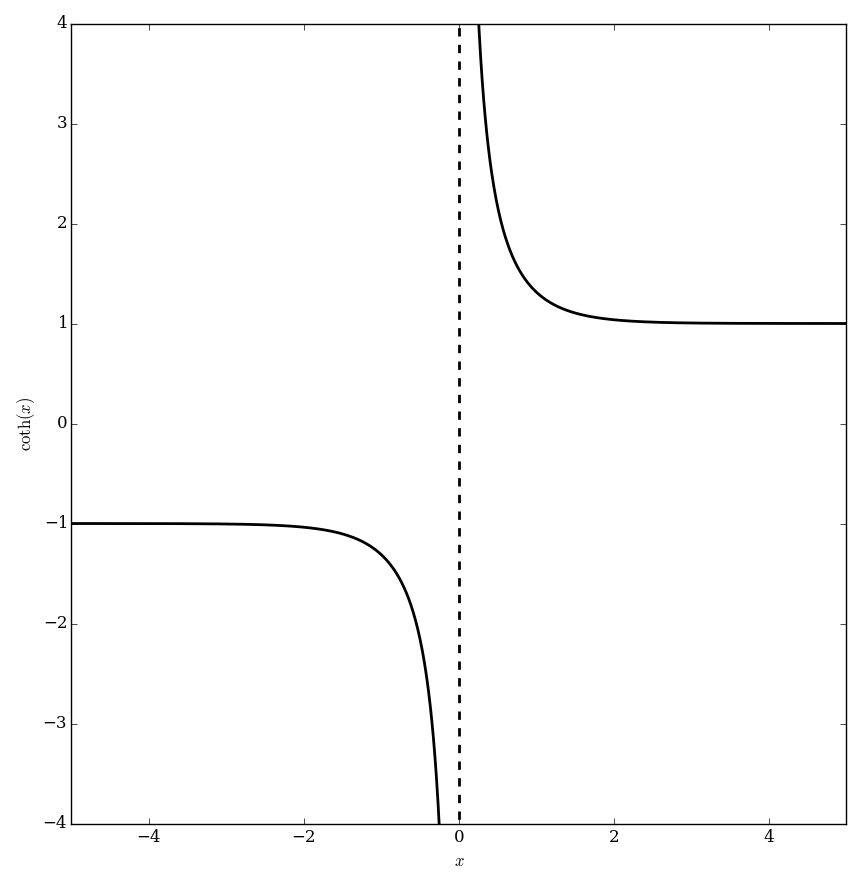
The hyperbolic cotangent is defined by $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)}=\dfrac{\mathrm{cosh}(z)}{\mathrm{sinh}(z)},$$ where $\tanh$ denotes the hyperbolic tangent function.
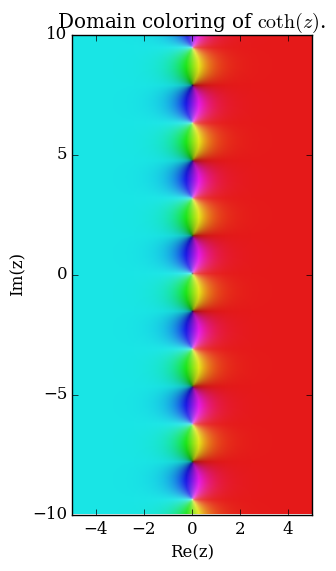
Domain coloring of $\mathrm{coth}$.
Properties
Derivative of coth
Antiderivative of coth
Relationship between coth and csch
Relationship between coth and cot
Relationship between cot and coth
Relationship between csc, Gudermannian, and coth
Relationship between coth, inverse Gudermannian, and csc
Pythagorean identity for coth and csch
Coth of a sum
z coth(z) = 2z/(e^(2z)-1) + z
z coth(z) = sum of 2^(2n)B_(2n) z^(2n)/(2n)!
z coth(z) = 2 Sum of (-1)^(n+1) zeta(2n) z^(2n)/pi^(2n)
Videos
Calculus I - Derivative of Hyperbolic Cotangent Function coth(x) - Proof
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.6$