Difference between revisions of "Jacobi theta 4"
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
$$\vartheta_4(z,q)=1+2\displaystyle\sum_{k=1}^{\infty} (-1)^k q^{k^2} \cos(2kz),$$ | $$\vartheta_4(z,q)=1+2\displaystyle\sum_{k=1}^{\infty} (-1)^k q^{k^2} \cos(2kz),$$ | ||
where $\cos$ denotes the [[cosine]] function. | where $\cos$ denotes the [[cosine]] function. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
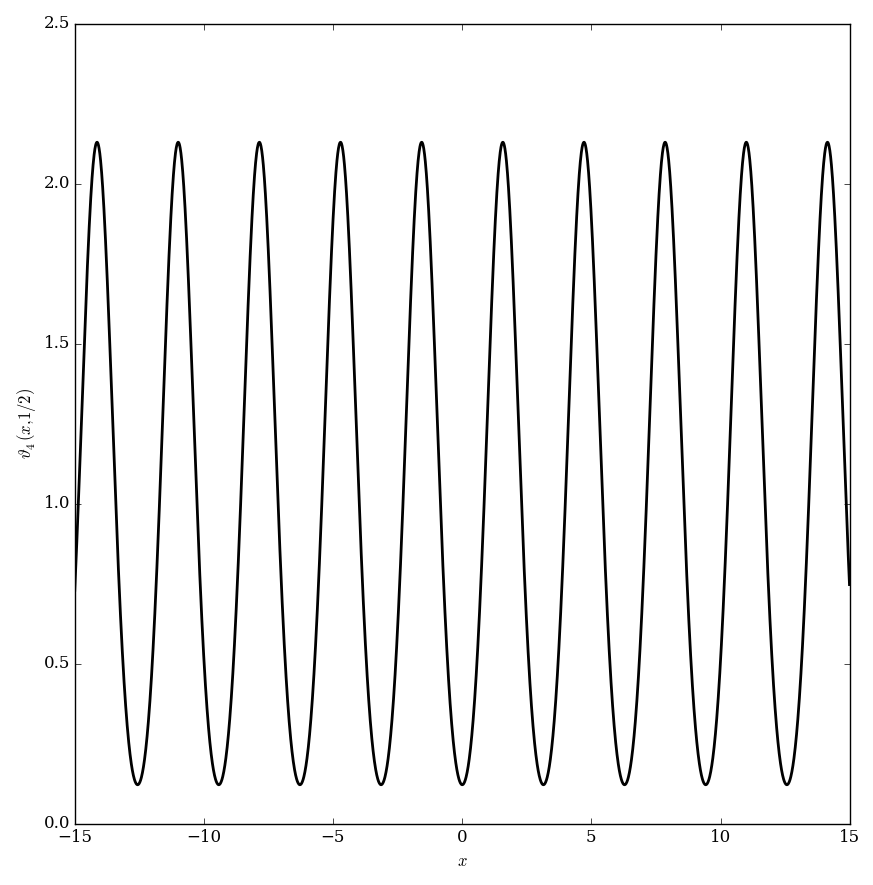
| + | File:Jacobitheta4,q=0.5plot.png|Graph of $\vartheta_4(z,\frac{1}{2})$. | ||
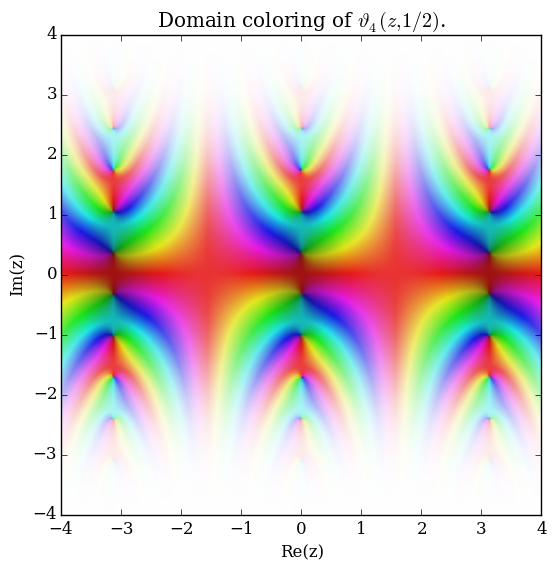
| + | File:Complexjacobitheta4,q=0.5plot.png|Domain coloring of $\vartheta_4 \left(z,\frac{1}{2} \right)$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| Line 11: | Line 18: | ||
[[Derivative of Jacobi theta 1 at 0]]<br /> | [[Derivative of Jacobi theta 1 at 0]]<br /> | ||
[[Logarithm of a quotient of Jacobi theta 4 equals a sum of sines]]<br /> | [[Logarithm of a quotient of Jacobi theta 4 equals a sum of sines]]<br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=References= | =References= | ||
* {{BookReference|Special Functions|1960|Earl David Rainville|prev=Jacobi theta 3|next=findme}}: $164. (4)$ | * {{BookReference|Special Functions|1960|Earl David Rainville|prev=Jacobi theta 3|next=findme}}: $164. (4)$ | ||
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Jacobi theta 3|next=Squares of theta relation for Jacobi theta 1 and Jacobi theta 4}}: $16.27.4$ | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Jacobi theta 3|next=Squares of theta relation for Jacobi theta 1 and Jacobi theta 4}}: $16.27.4$ | ||
| + | |||
| + | {{:Jacobi theta footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 20:24, 25 June 2017
Let $q \in \mathbb{C}$ with $|q|<1$. The Jacobi $\vartheta_4$ function is defined by $$\vartheta_4(z,q)=1+2\displaystyle\sum_{k=1}^{\infty} (-1)^k q^{k^2} \cos(2kz),$$ where $\cos$ denotes the cosine function.
Graph of $\vartheta_4(z,\frac{1}{2})$.
Domain coloring of $\vartheta_4 \left(z,\frac{1}{2} \right)$.
Properties
Squares of theta relation for Jacobi theta 1 and Jacobi theta 4
Squares of theta relation for Jacobi theta 2 and Jacobi theta 4
Squares of theta relation for Jacobi theta 3 and Jacobi theta 4
Squares of theta relation for Jacobi theta 4 and Jacobi theta 4
Sum of fourth powers of Jacobi theta 2 and Jacobi theta 4 equals fourth power of Jacobi theta 3
Derivative of Jacobi theta 1 at 0
Logarithm of a quotient of Jacobi theta 4 equals a sum of sines
References
- 1960: Earl David Rainville: Special Functions ... (previous) ... (next): $164. (4)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $16.27.4$
