Difference between revisions of "Spherical Hankel h (1)"

Revision as of 18:36, 24 May 2016

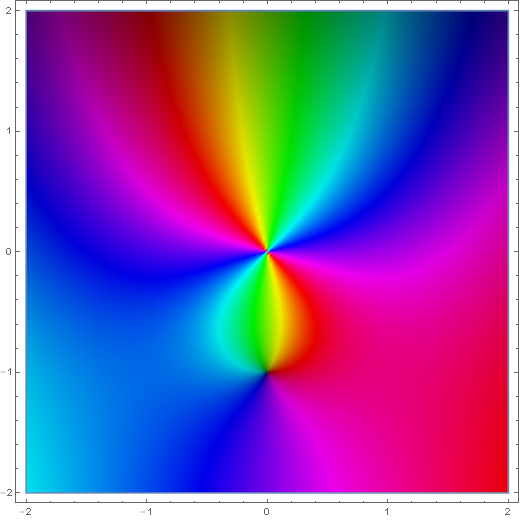
The spherical Hankel function $h_{\nu}^{(1)}$ is defined by $$h_{\nu}^{(1)}(z)=j_{\nu}(z)+iy_{\nu}(z),$$ where $j_{\nu}$ is the spherical Bessel function of the first kind and $y_{\nu}$ is the spherical Bessel function of the second kind.

Anger function

Bessel-Clifford

Bessel $J_{\nu}$

Bessel $Y_{\nu}$

Bessel $I_{\nu}$

Modified Bessel $K_{\nu}$

Spherical Bessel $j_{\nu}$

Spherical Bessel $y_{\nu}$