Difference between revisions of "Cosine"
From specialfunctionswiki
(→Properties) |
|||
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of cosine]] | |
| − | + | [[Taylor series of cosine]] | |
| − | + | [[Weierstrass factorization of cosine]] | |
| − | + | [[Beta in terms of sine and cosine]] | |
| − | + | [[Relationship between cosine and hypergeometric 0F1]] | |
| − | + | [[Relationship between spherical Bessel y sub nu and cosine]] | |
| − | + | [[Relationship between cosh and cos]] | |
| − | + | [[Relationship between cos and cosh]] | |
| − | + | [[Relationship between cosine, Gudermannian, and sech]] | |
| − | + | [[Relationship between sech, inverse Gudermannian, and cos]] | |
=See Also= | =See Also= | ||
Revision as of 00:42, 4 June 2016
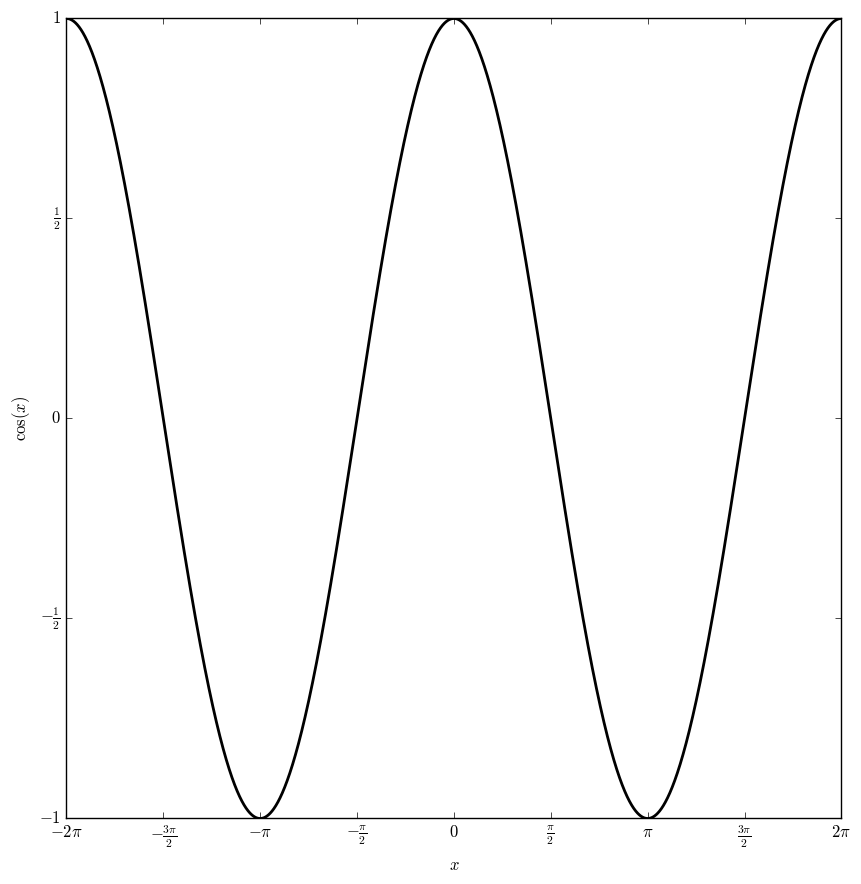
The cosine function, $\cos \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula $$\cos(z)=\dfrac{e^{iz}+e^{-iz}}{2},$$ where $e^z$ is the exponential function.
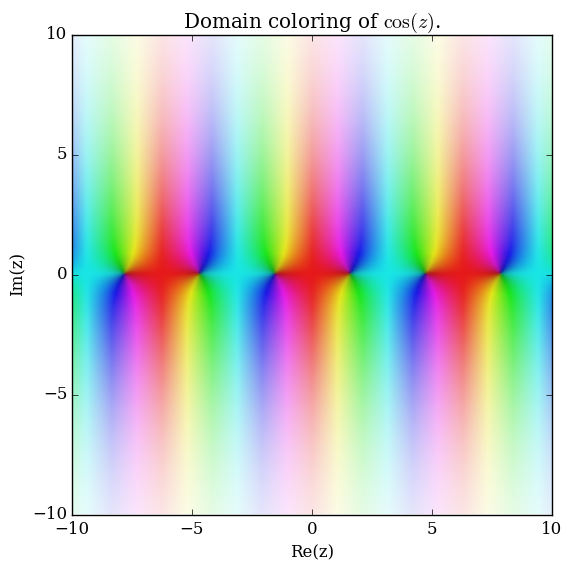
Domain coloring of $\cos$.
Properties
Derivative of cosine Taylor series of cosine Weierstrass factorization of cosine Beta in terms of sine and cosine Relationship between cosine and hypergeometric 0F1 Relationship between spherical Bessel y sub nu and cosine Relationship between cosh and cos Relationship between cos and cosh Relationship between cosine, Gudermannian, and sech Relationship between sech, inverse Gudermannian, and cos