Difference between revisions of "Secant"
| Line 18: | Line 18: | ||
[[Sech]] <br /> | [[Sech]] <br /> | ||
[[Arcsech]] <br /> | [[Arcsech]] <br /> | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Cosine|next=Tangent}}: 4.3.147 | ||
<center>{{:Trigonometric functions footer}}</center> | <center>{{:Trigonometric functions footer}}</center> | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 04:34, 6 June 2016
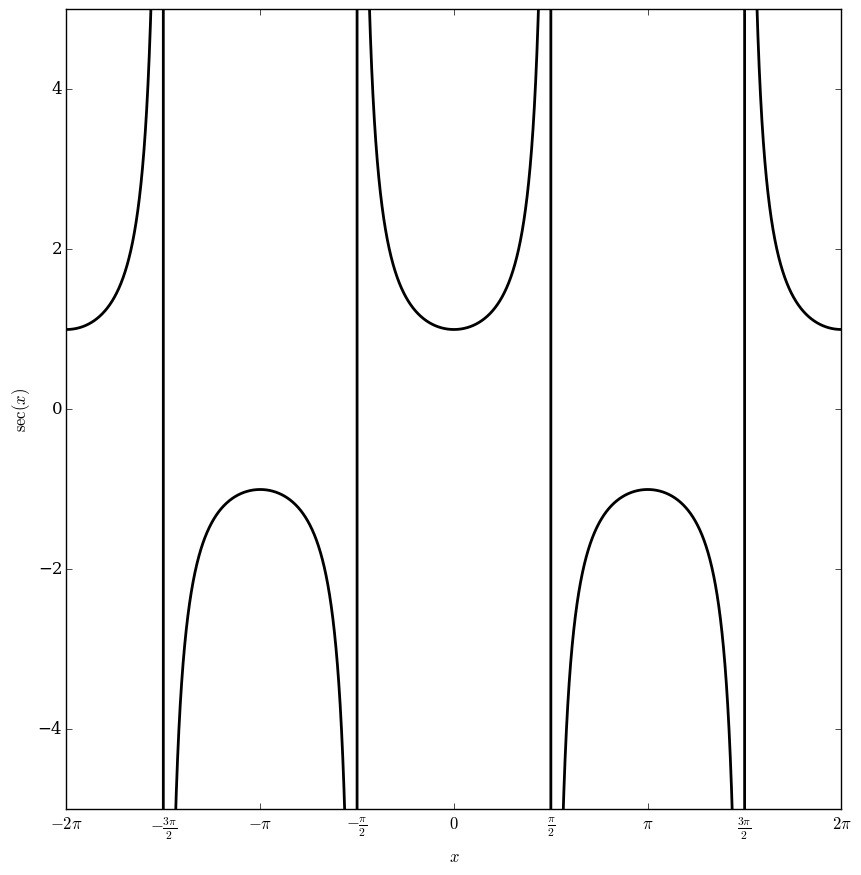
The secant function is defined by $$\sec(z)=\dfrac{1}{\cos(z)}.$$
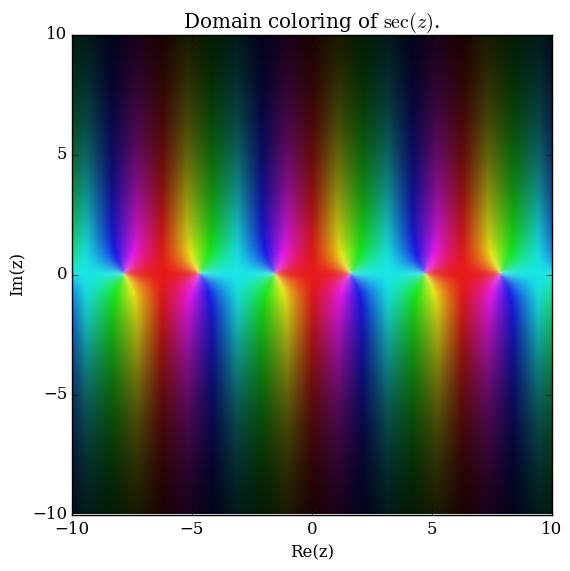
Domain coloring of $\sec$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \sec(z)=\tan(z)\sec(z),$$ where $\sec$ denotes the secant and $\cot$ denotes the cotangent.
Proof
From the definition of secant, $$\sec(z) = \dfrac{1}{\cos(z)},$$ and so using the quotient rule, the derivative of cosine, and the definition of tangent, $$\dfrac{\mathrm{d}}{\mathrm{d}z} \sec(z) = \dfrac{\mathrm{d}}{\mathrm{d}z} \dfrac{1}{\cos(z)} = \dfrac{\sin(z)}{\cos^2(z)}=\tan(z)\sec(z),$$ as was to be shown. $\blacksquare$
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.3.109$
Theorem
The following formula holds: $$\sec(\mathrm{gd}(x))=\cosh(x),$$ where $\sec$ denotes the secant, $\mathrm{gd}$ denotes the Gudermannian, and $\cosh$ denotes the hyperbolic cosine.
Proof
References
Theorem
The following formula holds: $$\cosh(\mathrm{gd}^{-1}(x))=\sec(x),$$ where $\cosh$ is the hyperbolic cosine, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\sec$ is the secant.
Proof
References
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.3.147