Difference between revisions of "Hankel H (2)"
From specialfunctionswiki
| Line 13: | Line 13: | ||
[[Bessel Y|Bessel $Y$]]<br /> | [[Bessel Y|Bessel $Y$]]<br /> | ||
| − | + | =References= | |
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Hankel H (1) in terms of csc and Bessel J|next=Hankel H (2) in terms of csc and Bessel J}}: 9.1.4 | ||
| + | |||
| + | {{:Hankel functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 04:12, 11 June 2016
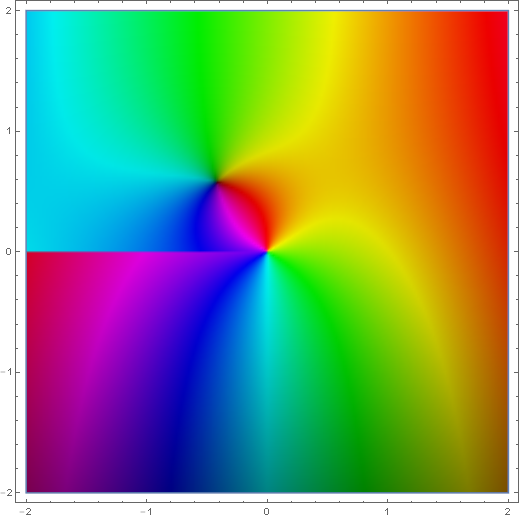
The Hankel functions of the second kind are defined by $$H_{\nu}^{(2)}(z)=J_{\nu}(z)-iY_{\nu}(z),$$ where $J_{\nu}$ is the Bessel function of the first kind and $Y_{\nu}$ is the Bessel function of the second kind. Note the similarity of these functions to the Hankel functions of the first kind.
Domain coloring of analytic continuation of $H_1^{(2)}(z)$.
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 9.1.4
Hankel $H_{\nu}^{(2)}$