Difference between revisions of "Struve function"
From specialfunctionswiki
| Line 1: | Line 1: | ||
The Struve functions are defined by | The Struve functions are defined by | ||
| − | $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma(k+\nu+\frac{3}{2})}$$ | + | $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma(k+\nu+\frac{3}{2})}.$$ |
<div align="center"> | <div align="center"> | ||
Revision as of 23:53, 21 October 2017
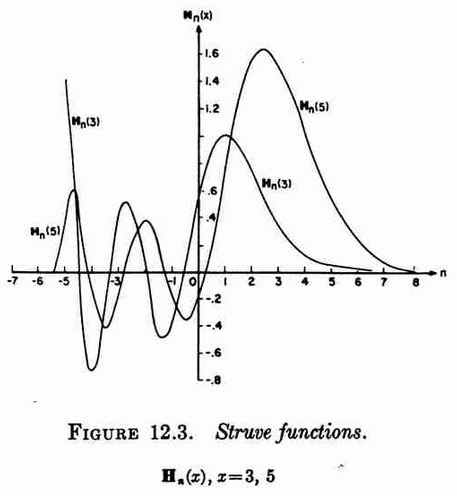
The Struve functions are defined by $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma(k+\nu+\frac{3}{2})}.$$
Properties
Relationship between Struve function and hypergeometric pFq
Relationship between Weber function 0 and Struve function 0
Relationship between Weber function 1 and Struve function 1