Difference between revisions of "Darboux function"
From specialfunctionswiki
| Line 14: | Line 14: | ||
=References= | =References= | ||
| − | + | * {{BookReference|Continuous Nowhere Differentiable Functions|2003|Johan Thim|prev=findme|next=findme}} $\S 3.5$, pg. 28 | |
{{:Continuous nowhere differentiable functions footer}} | {{:Continuous nowhere differentiable functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 18:01, 25 June 2017
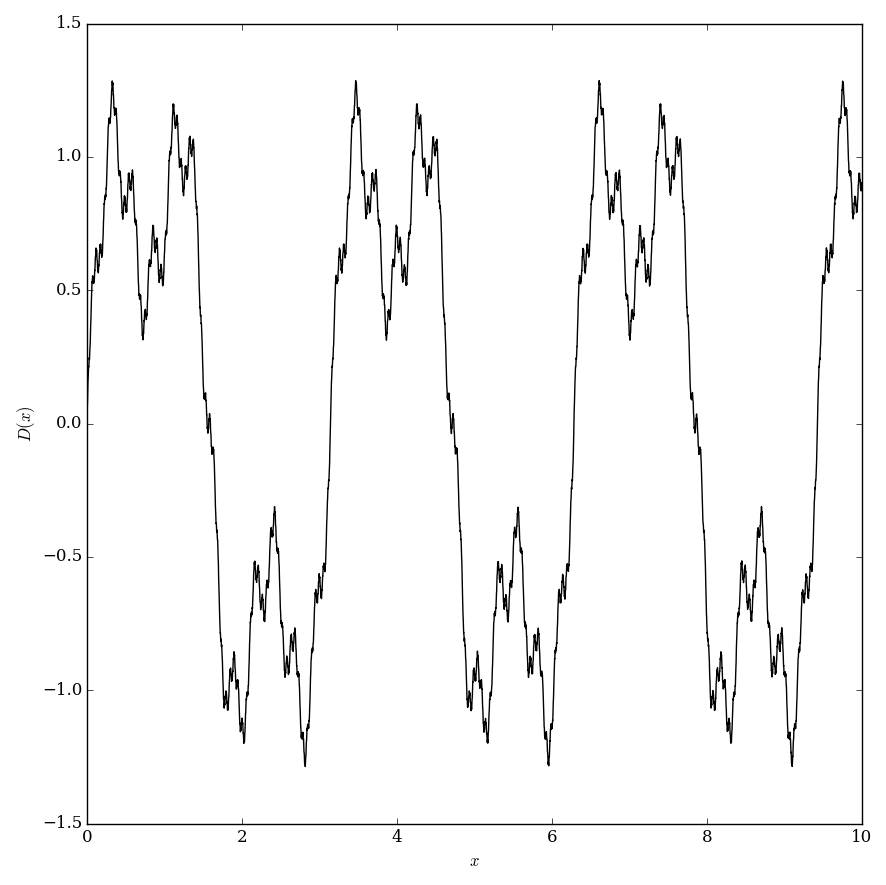
The Darboux function is defined by $$D(x)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\sin\left((k+1)!x\right)}{k!},$$ where $\sin$ denotes the sine function.
Properties
Darboux function is continuous
Darboux function is nowhere differentiable
References
- 2003: Johan Thim: Continuous Nowhere Differentiable Functions ... (previous) ... (next) $\S 3.5$, pg. 28