Difference between revisions of "Riemann zeta"
From specialfunctionswiki
| Line 34: | Line 34: | ||
* {{BookReference|The Zeta-Function of Riemann|1930|Edward Charles Titchmarsh|next=Euler product for Riemann zeta}}: § Introduction (1) | * {{BookReference|The Zeta-Function of Riemann|1930|Edward Charles Titchmarsh|next=Euler product for Riemann zeta}}: § Introduction (1) | ||
* {{BookReference|Higher Transcendental Functions Volume III|1953|Harry Bateman|prev=findme|next=Euler product for Riemann zeta}}: pg. $170$ | * {{BookReference|Higher Transcendental Functions Volume III|1953|Harry Bateman|prev=findme|next=Euler product for Riemann zeta}}: pg. $170$ | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Euler product for Riemann zeta}}: $23.2.1$ | ||
{{:Number theory functions footer}} | {{:Number theory functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 01:32, 13 July 2016
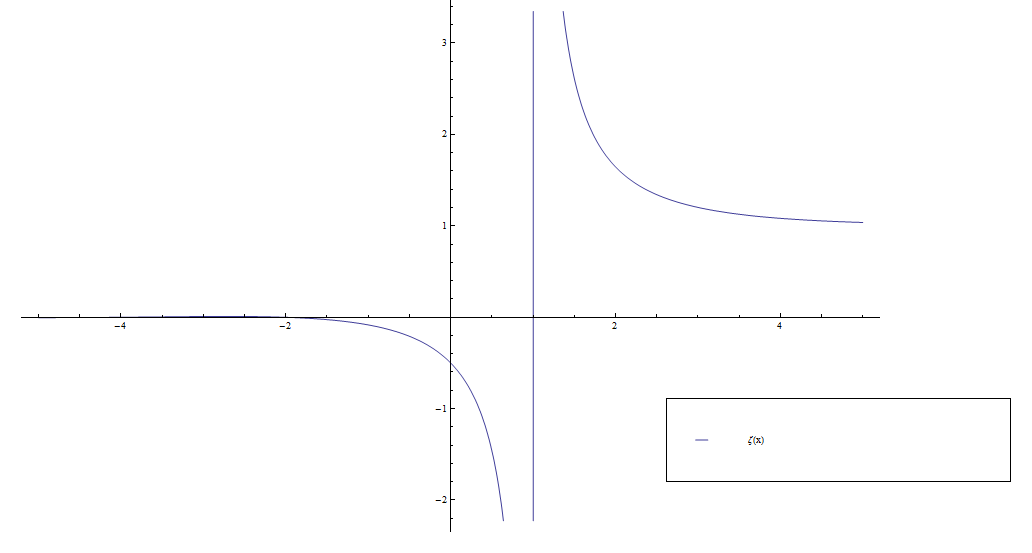
Consider the function $\zeta$ defined by the following series for $\mathrm{Re}(z)>1$: $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z}.$$
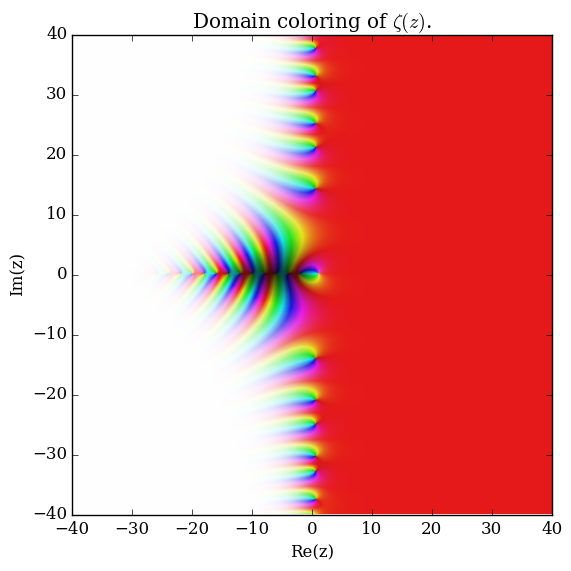
Domain coloring of $\zeta$.
Properties
Euler product for Riemann zeta
Laurent series of the Riemann zeta function
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
Series for log(riemann zeta) over primes
Series for log(Riemann zeta) in terms of Mangoldt function
Logarithmic derivative of Riemann zeta in terms of series over primes
Logarithmic derivative of Riemann zeta in terms of Mangoldt function
Videos
Riemann Zeta function playlist
Möbius Inversion of $\zeta(s)$
Zeta Integral
External links
- 15 Videos about the Riemann $\zeta$ function
- English translation of Riemann's paper "On the number of prime numbers less than a given quantity"
- Evaluating $\zeta(2)$
- The Riemann Hypothesis: FAQ and resources
- How Euler discovered the zeta function
- Andrew Odlyzko: Tables of zeros of the Riemann zeta function
References
- 1930: Edward Charles Titchmarsh: The Zeta-Function of Riemann ... (next): § Introduction (1)
- 1953: Harry Bateman: Higher Transcendental Functions Volume III ... (previous) ... (next): pg. $170$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $23.2.1$