Difference between revisions of "Chebyshev theta function"
From specialfunctionswiki
| Line 6: | Line 6: | ||
<gallery> | <gallery> | ||
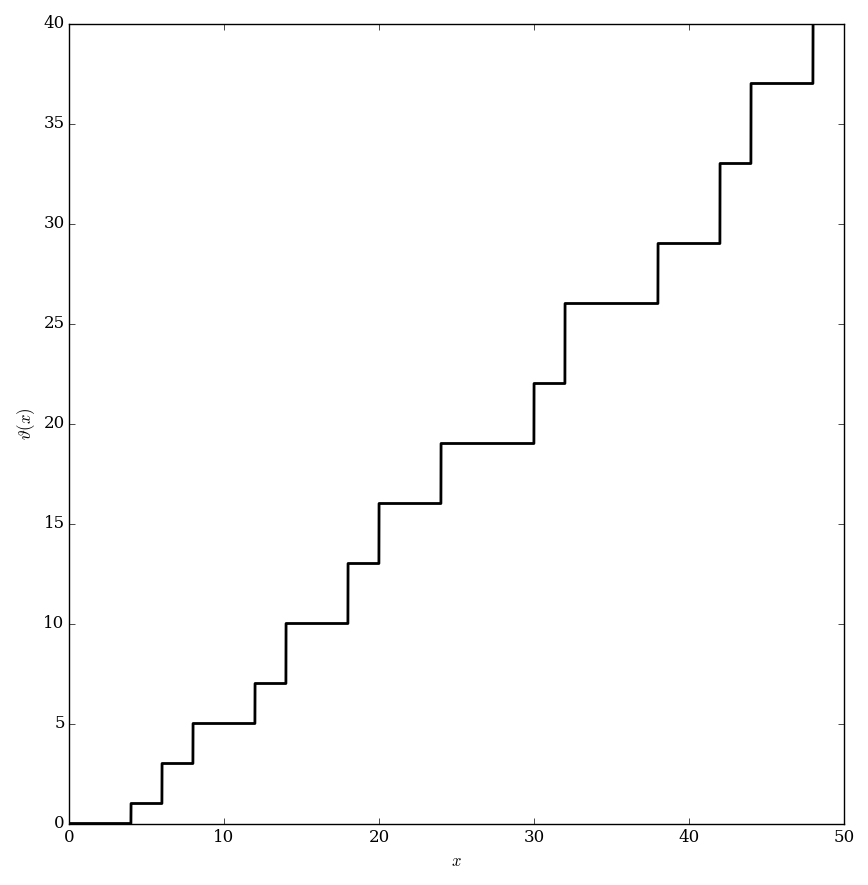
File:Chebyshevplotfrom0to50.png|Plot of $\vartheta$ on $[0,50]$. | File:Chebyshevplotfrom0to50.png|Plot of $\vartheta$ on $[0,50]$. | ||
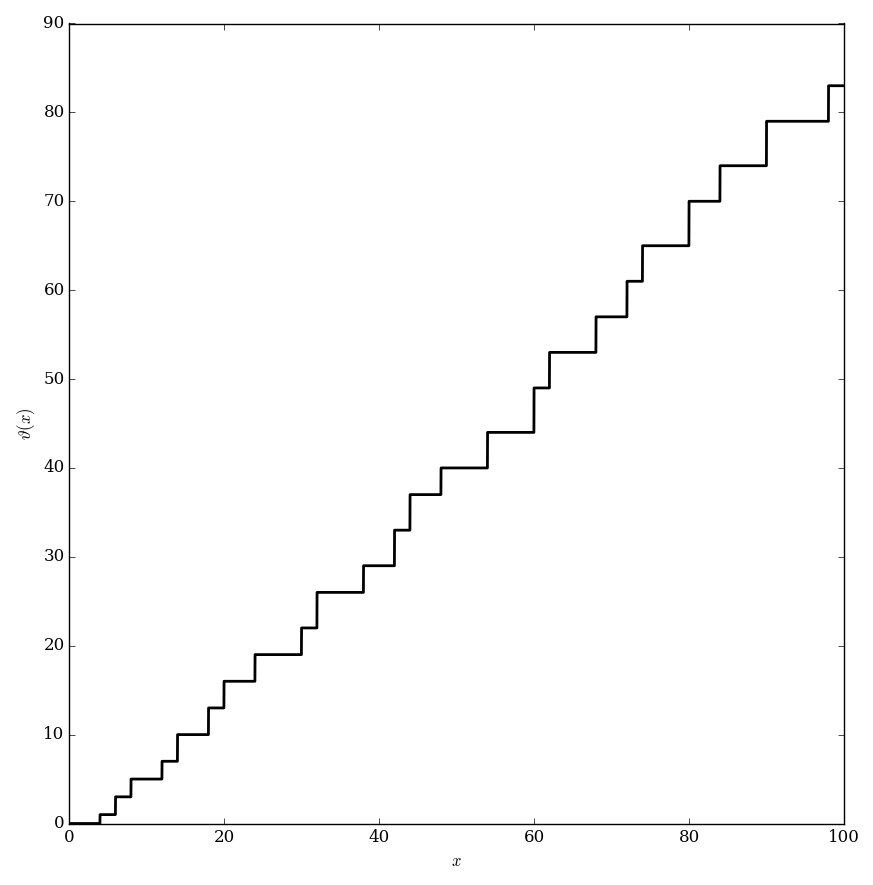
| − | File: | + | File:Chebyshevplotfrom0to100.png|Plot of $\vartheta$ on $[0,100]$. |
File:Chebyshevthetaplotto1000.png|Plot of $\vartheta$ on $[0,1000]$. | File:Chebyshevthetaplotto1000.png|Plot of $\vartheta$ on $[0,1000]$. | ||
</gallery> | </gallery> | ||
Revision as of 02:11, 28 November 2016
The Chebyshev $\vartheta$ function is $$\vartheta(x) = \displaystyle\sum_{p \leq x} \log p,$$ where $p \leq x$ denotes that $p$ is a prime number less than the real number $x$.
Plot of $\vartheta$ on $[0,50]$.
Plot of $\vartheta$ on $[0,100]$.
- Chebyshevthetaplotto1000.png
Plot of $\vartheta$ on $[0,1000]$.
