Difference between revisions of "Jacobi theta 1"
From specialfunctionswiki
| Line 18: | Line 18: | ||
[[Derivative of Jacobi theta 1 at 0]]<br /> | [[Derivative of Jacobi theta 1 at 0]]<br /> | ||
[[Logarithm of quotient of Jacobi theta 1 equals the log of a quotient of sines + a sum of sines]]<br /> | [[Logarithm of quotient of Jacobi theta 1 equals the log of a quotient of sines + a sum of sines]]<br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=References= | =References= | ||
| Line 28: | Line 23: | ||
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Jacobi theta 2}}: $16.27.1$ | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Jacobi theta 2}}: $16.27.1$ | ||
| + | {{:Jacobi theta footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 20:23, 25 June 2017
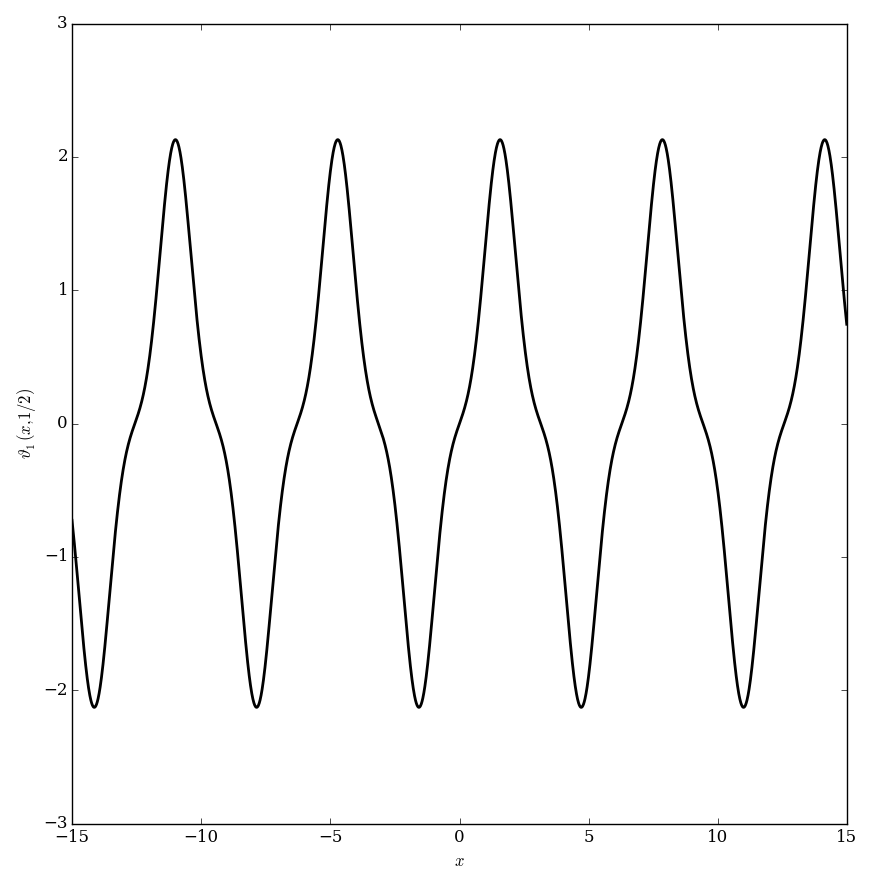
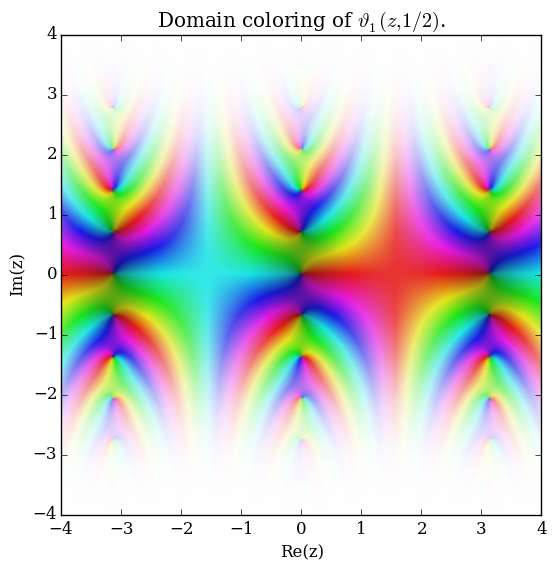
Let $q \in \mathbb{C}$ with $|q|<1$. The Jacobi $\vartheta_1$ function is defined by $$\vartheta_1(z,q)=2q^{\frac{1}{4}} \displaystyle\sum_{k=0}^{\infty} (-1)^k q^{k(k+1)} \sin((2k+1)z),$$ where $\sin$ denotes the sine function.
Graph of $\vartheta_1(z,\frac{1}{2})$.
Domain coloring of $\vartheta_1 \left(z,\frac{1}{2} \right)$.
Properties
Squares of theta relation for Jacobi theta 1 and Jacobi theta 4
Squares of theta relation for Jacobi theta 2 and Jacobi theta 4
Squares of theta relation for Jacobi theta 3 and Jacobi theta 4
Sum of fourth powers of Jacobi theta 2 and Jacobi theta 4 equals fourth power of Jacobi theta 3
Derivative of Jacobi theta 1 at 0
Logarithm of quotient of Jacobi theta 1 equals the log of a quotient of sines + a sum of sines
References
- 1960: Earl David Rainville: Special Functions ... (previous) ... (next): $164. (1)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $16.27.1$
