Difference between revisions of "Gamma"
(→References) |
|||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | The gamma function $\Gamma \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is the function initially defined for $ | + | The gamma function $\Gamma \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is the function initially defined for $\mathrm{Re}(z)>0$ by the integral by the formula |
| − | $$\Gamma( | + | $$\Gamma(z)=\displaystyle\int_0^{\infty} \xi^{z-1}e^{-\xi} \mathrm{d}\xi.$$ |
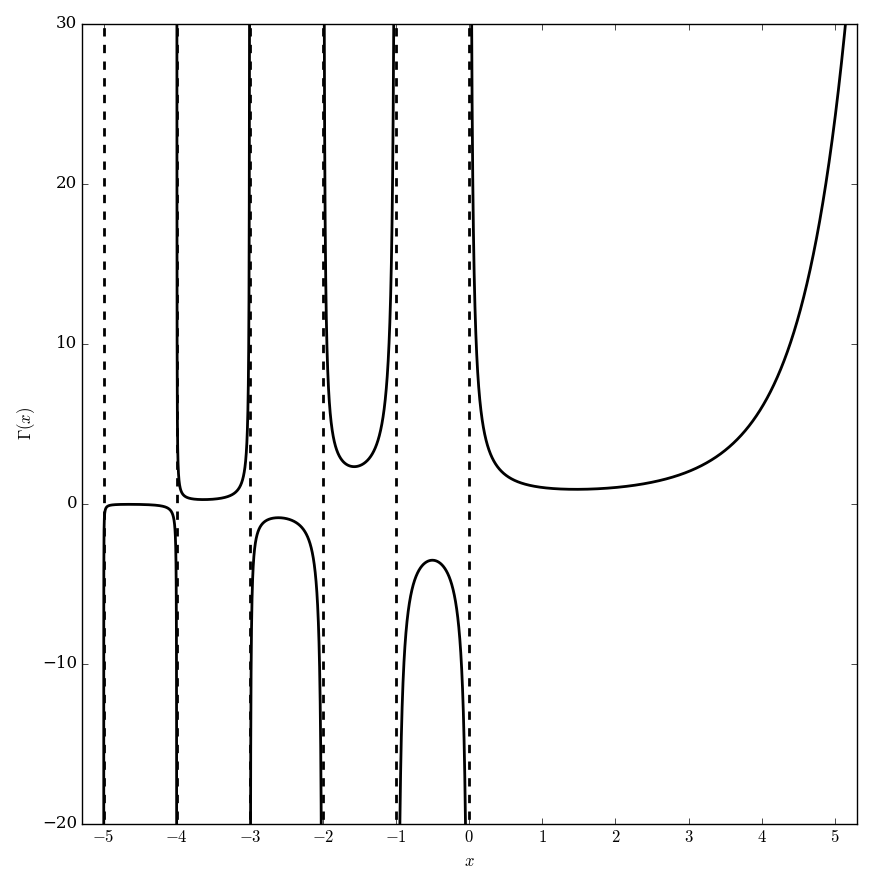
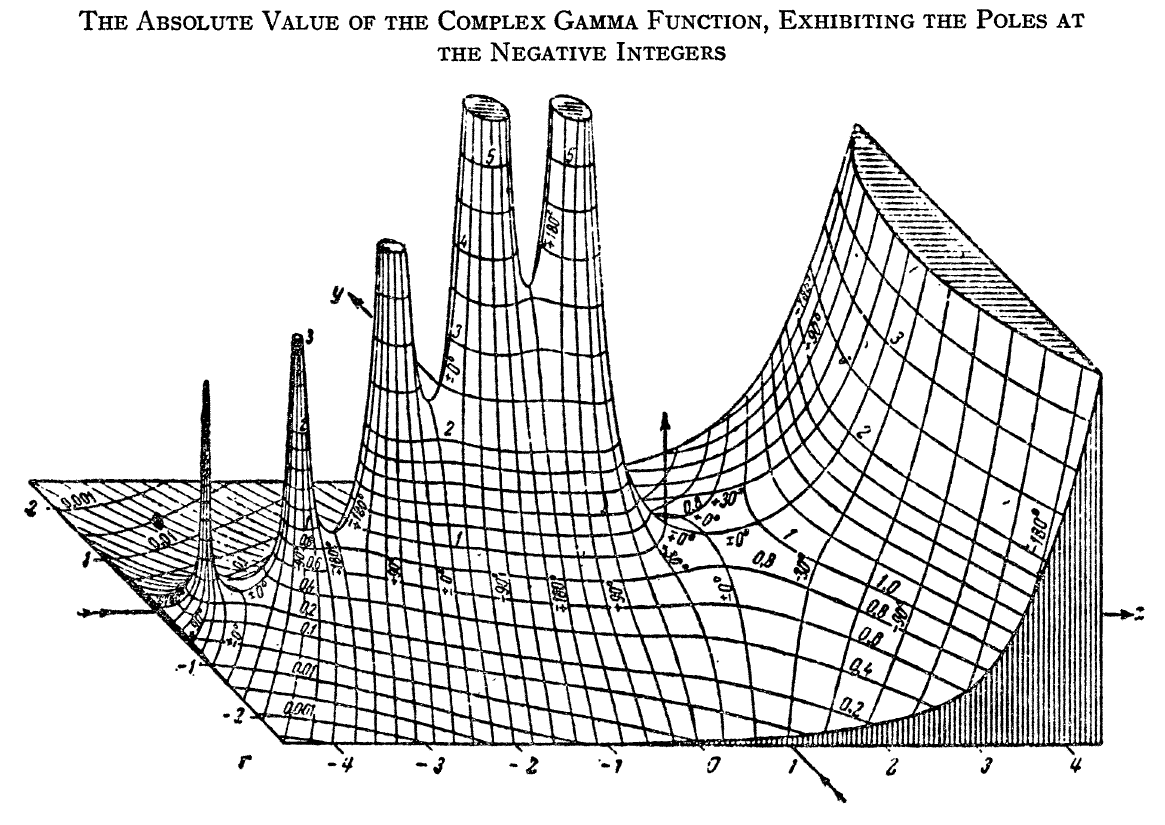
The [[analytic continuation]] of $\Gamma$ leads to a [[meromorphic function]] with [[pole | poles]] at the negative integers. | The [[analytic continuation]] of $\Gamma$ leads to a [[meromorphic function]] with [[pole | poles]] at the negative integers. | ||
Revision as of 23:16, 2 June 2017
The gamma function $\Gamma \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is the function initially defined for $\mathrm{Re}(z)>0$ by the integral by the formula $$\Gamma(z)=\displaystyle\int_0^{\infty} \xi^{z-1}e^{-\xi} \mathrm{d}\xi.$$ The analytic continuation of $\Gamma$ leads to a meromorphic function with poles at the negative integers.
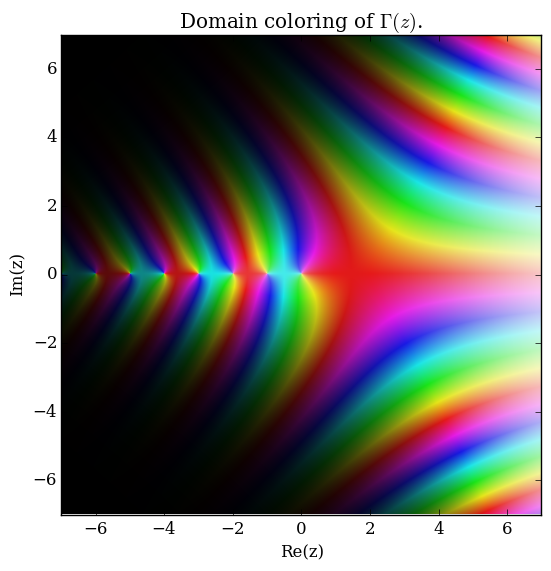
Domain coloring of $\Gamma$.
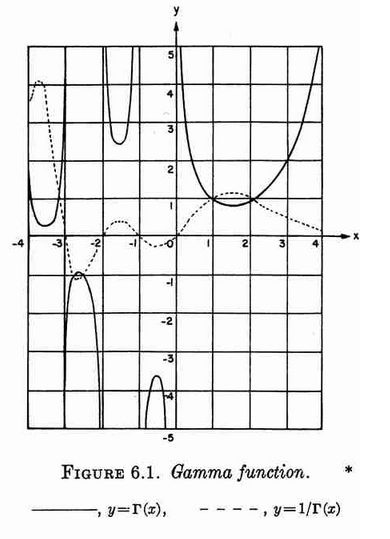
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
Properties
Gamma(z) as integral of a power of log(1/t) for Re(z) greater than 0
Gamma function written as a limit of a factorial, exponential, and a rising factorial
Gamma function written as infinite product
Value of Gamma(1)
Factorial property of gamma
Gamma at positive integers
Relationship between Hurwitz zeta and gamma function
Gamma-Sine Relation
Bohr-Mollerup theorem
Videos
What's the Gamma Function? (16 September 2008)
Gamma Function Of One-Half: Part 1 (10 August 2010)
Gamma Function Of One-Half: Part 2 (10 August 2010)
Gamma Integral Function - Introduction (5 December 2011)
gamma function - Part 1 (9 February 2012)
Gamma Function (playlist) (26 February 2012)
Gamma function (20 October 2012)
Beta Function, Gamma Function and their Properties (17 August 2013)
Thermodynamics 19 a : Gamma Function 1/2 (31 August 2013)
euler gamma function (14 September 2013)
The Gamma Function: intro (5) (13 February 2014)
The Gamma Function: why 0!=1 (5) (13 February 2014)
Mod-04 Lec-09 Analytic continuation and the gamma function (Part I) (3 June 2014)
Gamma function at 1/2 (3 January 2015)
Contour Integral Definition of the Gamma Function (18 January 2015)
External links
The sine product formula and the gamma function
Leonhard Euler's Integral: A Historical Profile of the Gamma Function
See Also
Loggamma
Polygamma
Reciprocal gamma
References
- 1895: Johann Heinrich Graf: Einleitung in die Theorie der Gammafunktion und der Euler'schen Integrale ... (previous) ... (next): $\S 3 (15_a)$
- 1920: Edmund Taylor Whittaker and George Neville Watson: A course of modern analysis ... (previous) ... (next): $\S 12 \cdot 1$
- 1953: Harry Bateman: Higher Transcendental Functions Volume I ... (next): $\S 1.1 (1)$
- 1960: Earl David Rainville: Special Functions ... (previous) ... (next): $15.(1)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $6.1.1$
- 1969: Yudell L. Luke: The Special Functions And Their Approximations, Volume I ... (previous) ... (next) $2.1 (1)$