Difference between revisions of "Cosh"
From specialfunctionswiki
| Line 29: | Line 29: | ||
[[Halving identity for sinh]]<br /> | [[Halving identity for sinh]]<br /> | ||
[[Halving identity for cosh]]<br /> | [[Halving identity for cosh]]<br /> | ||
| + | [[Halving identity for tangent (1)]]<br /> | ||
=See Also= | =See Also= | ||
Revision as of 23:41, 21 October 2017
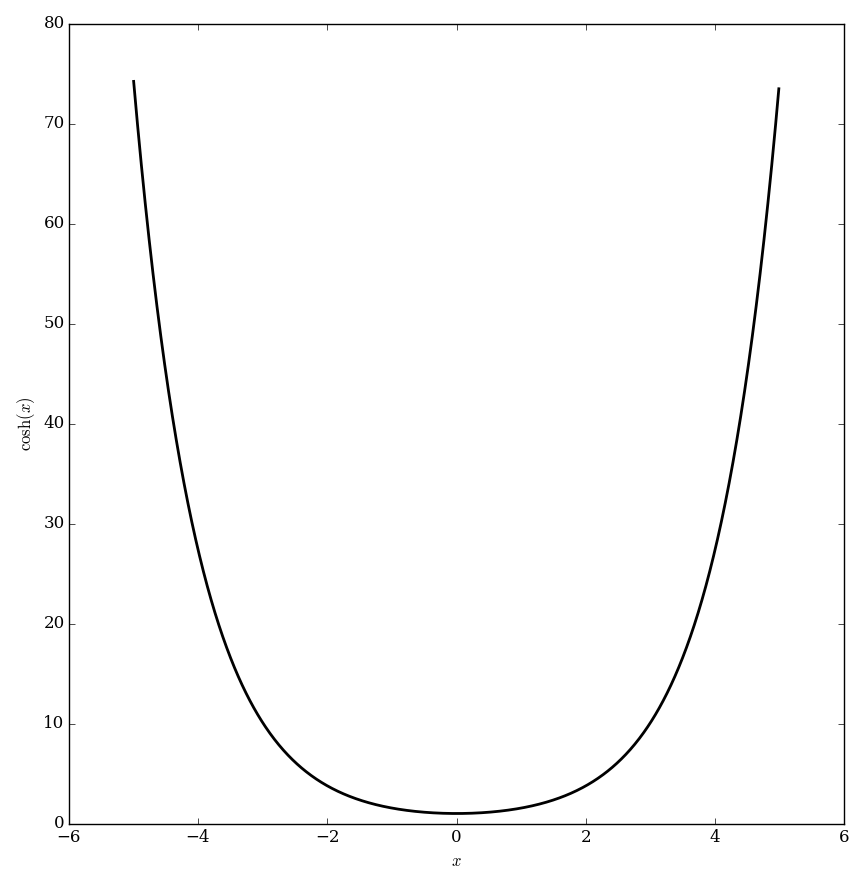
The hyperbolic cosine function $\cosh \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by
$$\mathrm{cosh}(z)=\dfrac{e^z + e^{-z}}{2}.$$
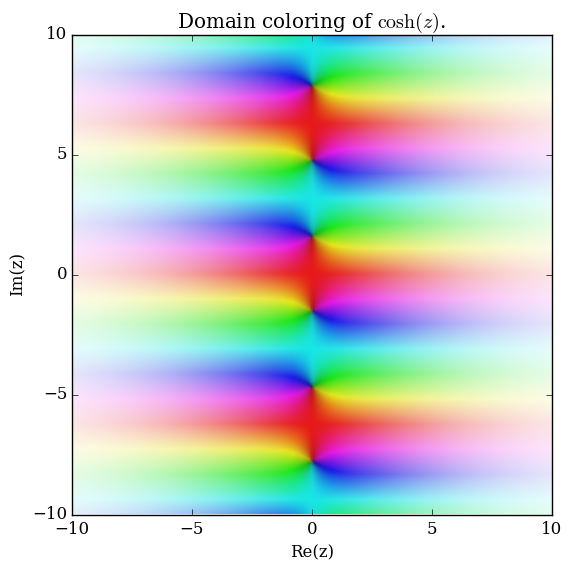
Domain coloring of analytic continuation of $\cosh$.
Properties
Derivative of cosh
Pythagorean identity for sinh and cosh
Weierstrass factorization of cosh
Relationship between cosh and hypergeometric 0F1
Relationship between Bessel I sub 1/2 and cosh
Relationship between cosh and cos
Relationship between cos and cosh
Relationship between secant, Gudermannian, and cosh
Relationship between cosh, inverse Gudermannian, and sec
Period of cosh
Sum of cosh and sinh
Difference of cosh and sinh
Cosh is even
Sinh of a sum
Cosh of a sum
Halving identity for sinh
Halving identity for cosh
Halving identity for tangent (1)
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.2$