Difference between revisions of "Riemann xi"
From specialfunctionswiki
(Created page with "The Riemann $\xi$ function is defined by the formula $$\xi(z)=\dfrac{z}{2}(z-1)\pi^{-\frac{z}{2}}\Gamma\left(\dfrac{z}{2}\right)\zeta(s),$$ where $\Gamma$ denotes the gamma...") |
m (Tom moved page Riemann xi function to Riemann xi) |
(No difference)
| |
Revision as of 08:35, 19 January 2015
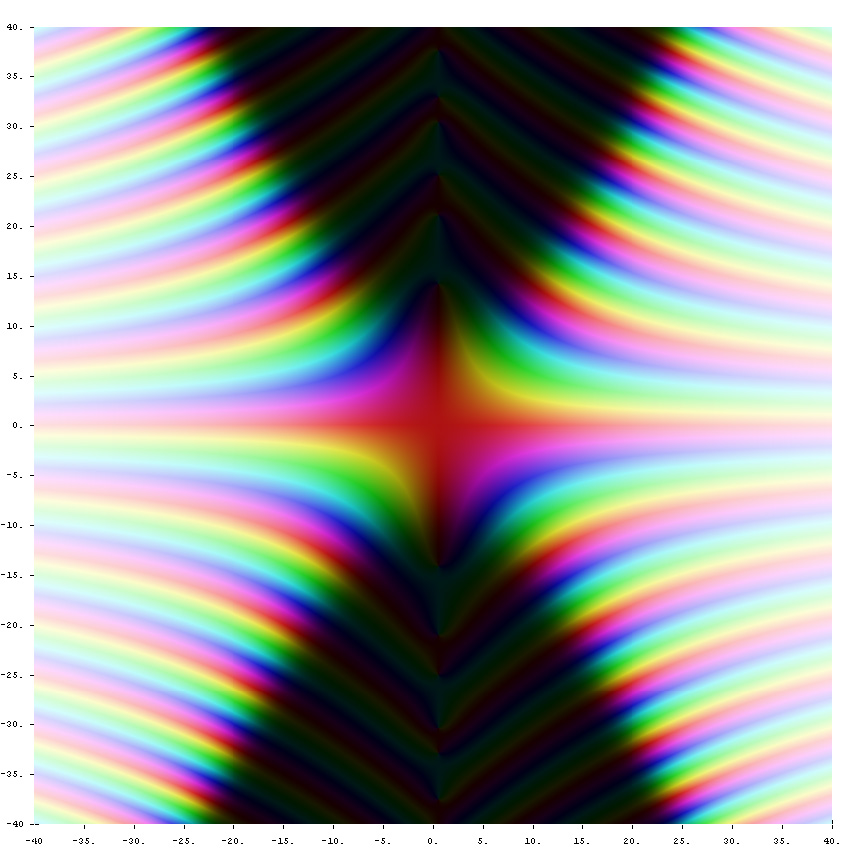
The Riemann $\xi$ function is defined by the formula $$\xi(z)=\dfrac{z}{2}(z-1)\pi^{-\frac{z}{2}}\Gamma\left(\dfrac{z}{2}\right)\zeta(s),$$ where $\Gamma$ denotes the gamma function and $\zeta$ denotes the Riemann zeta function.